题目内容
已知0<a<1,x=loga
+loga
,y=
loga5,z=loga
-loga
,则x,y,z的大小关系为
| 2 |
| 3 |
| 1 |
| 2 |
| 21 |
| 3 |
y>x>z
y>x>z
.分析:由0<a<1,知y=logax是减函数.再由x=loga
+loga
=loga
,y=
loga5=loga
,z=loga
-loga
=loga
,知y>x>z.
| 2 |
| 3 |
| 6 |
| 1 |
| 2 |
| 5 |
| 21 |
| 3 |
| 7 |
解答:解:∵0<a<1,
∴y=logax是减函数.
∵x=loga
+loga
=loga
,
y=
loga5=loga
,
z=loga
-loga
=loga
,
∴y>x>z.
故答案为:y>x>z.
∴y=logax是减函数.
∵x=loga
| 2 |
| 3 |
| 6 |
y=
| 1 |
| 2 |
| 5 |
z=loga
| 21 |
| 3 |
| 7 |
∴y>x>z.
故答案为:y>x>z.
点评:本题考查对数大小的比较,解题时要认真审题,注意对数函数的图象和性质的灵活运用.

练习册系列答案
相关题目
已知0<a<1,x=loga
+loga
,y=
loga5,z=loga
-loga
,则( )
| 2 |
| 3 |
| 1 |
| 2 |
| 21 |
| 3 |
| A、x>y>z |
| B、z>y>x |
| C、y>x>z |
| D、z>x>y |
已知0<a<1,x=loga
+loga
,y=loga
-loga
,z=
loga11,则( )
| 2 |
| 5 |
| 26 |
| 2 |
| 1 |
| 2 |
| A、x>y>z |
| B、x<y<z |
| C、x>z>y |
| D、y>x>z |
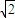 +loga
+loga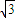 ,y=
,y= loga5,z=loga
loga5,z=loga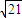 -loga
-loga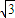 ,则( )
,则( )