题目内容
已知0<a<1,x=loga
+loga
,y=
loga5,z=loga
-loga
,则( )
| 2 |
| 3 |
| 1 |
| 2 |
| 21 |
| 3 |
| A、x>y>z |
| B、z>y>x |
| C、y>x>z |
| D、z>x>y |
分析:先化简x、y、z然后利用对数函数的单调性,比较大小即可.
解答:解:x=loga
+loga
=loga
,
y=
loga5=loga
,z=loga
-loga
=loga
,
∵0<a<1,又
<
<
,
∴loga
>loga
>loga
,即y>x>z.
故选 C.
| 2 |
| 3 |
| 6 |
y=
| 1 |
| 2 |
| 5 |
| 21 |
| 3 |
| 7 |
∵0<a<1,又
| 5 |
| 6 |
| 7 |
∴loga
| 5 |
| 6 |
| 7 |
故选 C.
点评:本题考查对数函数的性质,对数的化简,是基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知0<a<1,x=loga
+loga
,y=loga
-loga
,z=
loga11,则( )
| 2 |
| 5 |
| 26 |
| 2 |
| 1 |
| 2 |
| A、x>y>z |
| B、x<y<z |
| C、x>z>y |
| D、y>x>z |
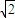 +loga
+loga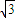 ,y=
,y= loga5,z=loga
loga5,z=loga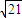 -loga
-loga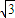 ,则( )
,则( )