题目内容
已知向量
，
，
中，2
-
=（
），
=（1，
），
=3，|
|=4，则
与
的夹角为 ．
【答案】分析：先根据已知条件求出（2
-
）•
，再结合
=3，|
|=4即可得到结论．
解答：解：因为：（2
-
）•
=2
-
=-1+3=2，
所以：
=4=|
|•|
|cosθ=4×2×cosθ
∴cosθ=
⇒θ=
．
故答案为：
．
点评：本题考查平面向量的基本运算性质，数量积的运算性质，考查向量问题的基本解法，等价转化思想．要区分向量运算与数的运算．避免类比数的运算进行错误选择．
-）•，再结合=3，||=4即可得到结论．解答：解：因为：（2
-）•=2-=-1+3=2，所以：
=4=||•||cosθ=4×2×cosθ∴cosθ=
⇒θ=．故答案为：
．点评：本题考查平面向量的基本运算性质，数量积的运算性质，考查向量问题的基本解法，等价转化思想．要区分向量运算与数的运算．避免类比数的运算进行错误选择．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
在平面直角坐标系中，已知向量
=（1，2），
-
=（3，1），c=（x，3），若（2
+
）∥
，则x=（ ）
| a |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| c |
| A、-2 | B、-4 | C、-3 | D、-1 |
，
，
中，2
），
），
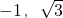=3，|