题目内容
 已知某四棱锥P-ABCD的三视图如图,E是侧棱PC上的动点.
已知某四棱锥P-ABCD的三视图如图,E是侧棱PC上的动点.(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)点E在线段PC上任意移动,是否总有BD⊥AE?证明你的结论.
分析:(I)根据三视图,可得四棱锥P-ABCD的底面为边长等于1的正方形,侧棱PC⊥平面ABCD,PC=2,由此利用锥体的体积公式,即可算出四棱锥P-ABCD的体积;
(II)由PC⊥平面ABCD证出BD⊥PC,结合正方形ABCD的对角线BD⊥AC,利用线面垂直判定定理证出BD⊥平面PAC,从而证出BD⊥AE.因此当E在线段PC上任意移动时,总有BD⊥AE.
(II)由PC⊥平面ABCD证出BD⊥PC,结合正方形ABCD的对角线BD⊥AC,利用线面垂直判定定理证出BD⊥平面PAC,从而证出BD⊥AE.因此当E在线段PC上任意移动时,总有BD⊥AE.
解答:解:(Ⅰ)由三视图,可知四棱锥P-ABCD的底面是一个正方形
正方形的边长这1,故SABCD=1 …(3分)
∴四棱锥P-ABCD的体积V=
SABCD•h=
×1×2=
cm3 …(7分)
(Ⅱ)结论:总有BD⊥AE …(8分)
证明:由三视图,可知PC⊥平面ABCD
∵BD?平面ABCD,∴BD⊥PC …(10分)
又∵在正方形中BD⊥AC …(12分)
且AC、PC是平面PAC内的两条相交直线
∴BD⊥平面PAC
∵AE?平面PAC,∴BD⊥AE …(14分)

正方形的边长这1,故SABCD=1 …(3分)
∴四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)结论:总有BD⊥AE …(8分)
证明:由三视图,可知PC⊥平面ABCD
∵BD?平面ABCD,∴BD⊥PC …(10分)
又∵在正方形中BD⊥AC …(12分)
且AC、PC是平面PAC内的两条相交直线
∴BD⊥平面PAC
∵AE?平面PAC,∴BD⊥AE …(14分)
点评:本题给出四棱锥的三视图,求它的体积并证明线线垂直.着重考查了三视图的认识、线面垂直的判定与性质和锥体的体积求法等知识,属于中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
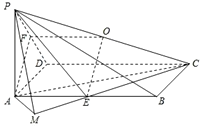 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.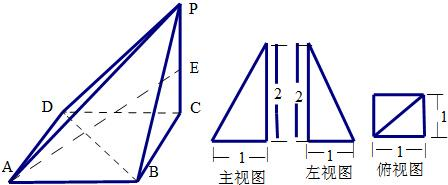 已知一四棱锥P-ABCD的三视图,E是侧棱PC上的动点.
已知一四棱锥P-ABCD的三视图,E是侧棱PC上的动点. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.