题目内容
已知正四棱锥P-ABCD中,PA=2| 3 |
分析:设出正四棱锥的底边a与高h并且根据题意得到a与h的关系,利用h表达出正四棱锥P-ABCD的体积,结合导数求解体积的最大值,进而得到高h的值.
解答:解:设正四棱锥P-ABCD的底面变长为a,高位h,
因为在正四棱锥P-ABCD中,PA=2
,
所以有
+h2=12,即a2=24-2h2.
所以正四棱锥P-ABCD的体积为:y=Vp-ABCD=
a2h=8h-
h3(h>0)
所以y′=8-2h2,令y′>0得0<h<2,令y′<0得h>2,
所以当h=2时正四棱锥P-ABCD的体积有最大值.
故答案为2.
因为在正四棱锥P-ABCD中,PA=2
| 3 |
所以有
| a2 |
| 2 |
所以正四棱锥P-ABCD的体积为:y=Vp-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
所以y′=8-2h2,令y′>0得0<h<2,令y′<0得h>2,
所以当h=2时正四棱锥P-ABCD的体积有最大值.
故答案为2.
点评:解决此类问题的关键是熟悉几何体的结构特征,正确记忆其体积公式并且能够灵活的利用导数解决最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
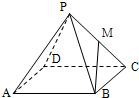
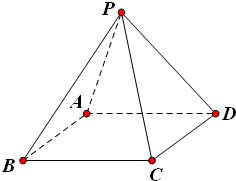 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h. ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .