Question

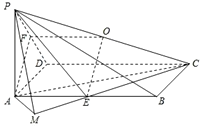已知在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD的中点．
（Ⅰ）求证：AF∥平面PEC；
（Ⅱ）求PC与平面ABCD所成角的正弦值；
（Ⅲ）求二面角P-EC-D的余弦值．

Answer 1

分析：（Ⅰ）取PC的中点O，连接OF，证出四边形AEOF是平行四边形，得出AF∥OE，则可证出AF∥平面PEC；
（Ⅱ）由已知，可证∠PCA是直线PC与平面ABCD所成的 角，在△PCA求其正弦值即可．
（Ⅲ）作AM⊥CE，交CE的延长线于M．连接PM，可得∠PMA是二面角P-EC-D的平面角，在△PMA中计算可得．

解答：解：（Ⅰ）取PC的中点O，连接OF、
OE．∴FO∥DC，且FO=

1

2

DC
∴FO∥AE             
又E是AB的中点．且AB=DC．∴FO=AE．
∴四边形AEOF是平行四边形．∴AF∥OE
又OE?平面PEC，AF?平面PEC
∴AF∥平面PEC       
（Ⅱ）连接AC
∵PA⊥平面ABCD，∴∠PCA是直线PC与平面ABCD所成的角      
在Rt△PAC中，tan∠PCA=

PA

AC

=

1

5

=

5

5

即直线PC与平面ABCD所成的角正弦值为

6

6

（Ⅲ）作AM⊥CE，交CE的延长线于M．连接PM，由三垂线定理．得PM⊥CE
∴∠PMA是二面角P-EC-D的平面角．      
由△AME∽△CBE，可得AM=

2

2

，∴tan∠PMA=

PA

AM

=

2

∴二面角P一EC一D的余弦值为 

6

6

点评：本小题主要考查空间线面关系、二面角、线面角的计算，考查化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力