题目内容

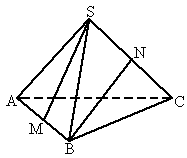
如图,S是正△ABC所在平面外一点,SA=SB=SC,且∠ASB=∠BSC=∠CSA=90°,M、N分别是AB和SC的中点,求异面直线SM与BN所成角的余弦值.

解:设正△ABC的边长为4a,

则SA=SB=SC=·AB=,

SM=AB=2a,

BN=.

如图,取MC的中点O,连结BO、NO,

则O=SM=a,OM=CM=,∠OMB=90°,∴OB=.

在△ONB中,cos∠BNO=.

∵ON∥SM,∴∠BNO是异面直线SM与BN所成的角,

即异面直线SM与BN所成角的余弦值为.

练习册系列答案
相关题目
如图1，在△ABC中AB⊥AC、AD⊥BC，D是垂足，则AB2=BD•BC（射影定理）．类似的有命题：在三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则（S△ABC）2=S△BCO•S△BCD（S表示面积．上述命题（　　）
精英家教网如图，在正四棱锥S-ABCD中，AB=8
2
，SA=10，M、N、O分别是SA、SB、BD的中点．
（1）设P是OC的中点，证明：PN∥平面BMD；
（2）求直线SO与平面BMD所成角的大小；
（3）在△ABC内是否存在一点G，使NG⊥平面BMD，若存在，求线段NG的长度；若不存在，说明理由．

如图，S是正△ABC所在平面外一点，SA=SB=SC，且∠ASB=∠BSC=∠CSA=90°，M，N分别是AB和SC的中点，求异面直线SM与BN所成角的余弦值．

如图，S是正△ABC所在平面外一点，SA=SB=SC，且∠ASB=∠BSC=∠CSA=90°，M，N分别是AB和SC的中点，求异面直线SM与BN所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网