题目内容
(本小题满分13分)设向量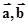 满足
满足 及
及
(1)求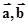 夹角的大小; (2)求
夹角的大小; (2)求 的值.
的值.
(1) .(2)|3a+b|=
.(2)|3a+b|= .
.
解析试题分析:(1)根据(3a-2b)2=7,9|a|2+4|b|2-12a·b=7,可得a·b= ,再根据数量积的定义可求出cos θ=
,再根据数量积的定义可求出cos θ= ,进而得到
,进而得到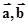 夹角.
夹角.
(2)先求(3a+b)2=9|a|2+6a·b+|b|2=9+3+1=13,从而得到|3a+b|= .
.
(1)设a与b夹角为θ,(3a-2b)2=7,9|a|2+4|b|2-12a·b=7,而|a|=|b|=1,
∴a·b= ,∴|a||b|cos θ=
,∴|a||b|cos θ= ,即cos θ=
,即cos θ=
又θ∈[0,π],∴a,b所成的角为 .
.
(2)(3a+b)2=9|a|2+6a·b+|b|2=9+3+1=13,
∴|3a+b|= ..
..
考点:考查了向量的数量积,以及利用数量积求模,夹角等知识.
点评:掌握数量积的定义: ,
,
求 模可利用:
模可利用: 来求解.
来求解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
平面向量 与
与 的夹角为60°,
的夹角为60°, ,
, ,则
,则 ( ).
( ).
| A.9 | B. | C.3 | D.7 |
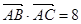 ,记
,记 ,△ABC的面积为
,△ABC的面积为 ,且满足
,且满足 .
. 的取值范围;
的取值范围; 的最大值和最小值.
的最大值和最小值. ,
, ,求x,y的值使
,求x,y的值使 ,且
,且 。
。 ,
, 与
与 夹角为
夹角为 ,求
,求 与
与 夹角的余弦值。
夹角的余弦值。 =(
=( +1,
+1, ),
), =(1,4cos(x
=(1,4cos(x +)),设函数
+)),设函数 =
= (
( ,则
,则 的取值范围是( )
的取值范围是( )




 ,则
,则 的取值范围为( )
的取值范围为( ) B.
B. C
C D
D