题目内容
2.已知F是抛物线x2=4y的焦点,P为抛物线上的动点,且A的坐标为(0,-1),则$\frac{|PF|}{|PA|}$的最小值是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 过点P作PM垂直于准线,M为垂足,则由抛物线的定义可得|PF|=|PM|,则$\frac{|PF|}{|PA|}$=$\frac{|PM|}{|PA|}$=sin∠PAM,∠PAM为锐角.故当PA和抛物线相切时,$\frac{|PF|}{|PA|}$最小.再利用直线的斜率公式、导数的几何意义求得切点的坐标,从而求得$\frac{|PF|}{|PA|}$的最小值.
解答 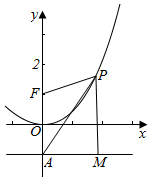 解:由题意可得,抛物线x2=4y的焦点F(0,1),
解:由题意可得,抛物线x2=4y的焦点F(0,1),
准线方程为y=-1.
过点P作PM垂直于准线,M为垂足,
则由抛物线的定义可得|PF|=|PM|,
则$\frac{|PF|}{|PA|}$=$\frac{|PM|}{|PA|}$=sin∠PAM,∠PAM为锐角.
故当∠PAM最小时,$\frac{|PF|}{|PA|}$最小,
故当PA和抛物线相切时,$\frac{|PF|}{|PA|}$最小.
设切点P(2$\sqrt{a}$,a),由y=$\frac{1}{4}$x2的导数为y′=$\frac{1}{2}$x,
则PA的斜率为$\frac{1}{2}$•2$\sqrt{a}$=$\sqrt{a}$=$\frac{a+1}{2\sqrt{a}}$,
求得a=1,可得P(2,1),
∴|PM|=2,|PA|=2$\sqrt{2}$,
∴sin∠PAM=$\frac{|PM|}{|PA|}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题主要考查抛物线的定义、性质的简单应用,直线的斜率公式、导数的几何意义,属于中档题.

练习册系列答案
相关题目
10.某校数学课外活动小组有高一学生10人,高二学生8人,高三学生7人,每一年级各选1名组长,不同的选法种数为( )
| A. | 25 | B. | 26 | C. | 560 | D. | 230 |
12.在数列{an}中,a1=1,an+1=$\frac{{a}_{n}+t}{{a}_{n}+1}$,则( )
| A. | 当t∈(0,1)时,{an}为递减数列 | B. | 当t∈(0,1)时,{an}为递增数列 | ||
| C. | 当t∈(1,+∞)时,{an}为递减数列 | D. | 当t∈(1,+∞)时,{an}为递增数列. |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)以双曲线x2-$\frac{{y}^{2}}{3}$=1的焦点为顶点,顶点为焦点,过点H(3,0)的直线与椭圆交于两点P(x1,y1)、Q(x2,y2),过Q作直线垂直于x轴,交椭圆于另一点R.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)以双曲线x2-$\frac{{y}^{2}}{3}$=1的焦点为顶点,顶点为焦点,过点H(3,0)的直线与椭圆交于两点P(x1,y1)、Q(x2,y2),过Q作直线垂直于x轴,交椭圆于另一点R.