题目内容
已知函数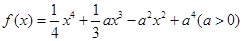
(1)求函数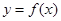 的单调区间;
的单调区间;
(2)若函数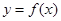 的图像与直线
的图像与直线 恰有两个交点,求
恰有两个交点,求 的取值范围.
的取值范围.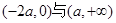
(1)递增区间为,递减区间为 (2)
(2) 或
或 .
.
解析试题分析:(1)利用导数求函数单调区间,关键明确定义域,正确求出导函数. 因为 ,令
,令 得
得 由
由 时,列表分析
时,列表分析 在
在 根的左右的符号,得
根的左右的符号,得 的递增区间为
的递增区间为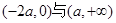 ,
, 的递减区间为
的递减区间为 ,(2)由(1)得到
,(2)由(1)得到 ,
,
 ,要使
,要使 的图像与直线
的图像与直线 恰有两个交点,只要
恰有两个交点,只要 或
或 ,即
,即 或
或 .
.
解:(1)因为 2分
2分
令 得
得
由 时,
时, 在
在 根的左右的符号如下表所示
根的左右的符号如下表所示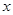














 练习册系列答案
练习册系列答案
王朝霞考点梳理时习卷系列答案
好成绩优佳必选卷系列答案
好成绩1加1优选好卷系列答案
黄冈状元成才路导学案系列答案

单元测试超效最新AB卷系列答案


海淀考王期末完胜100分系列答案
 相关题目
相关题目
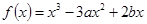 在x=1处有极小值-1,
在x=1处有极小值-1,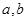 的值; (2)求出
的值; (2)求出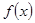 的单调区间.
的单调区间.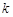
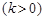 .现已知相距18
.现已知相距18 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为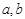 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数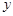 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设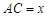 (
(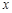 的函数; (2)若
的函数; (2)若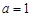 ,且
,且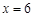 时,
时,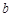 的值.
的值.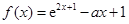 ,
,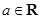 .
.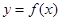 在点
在点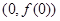 处的切线与直线
处的切线与直线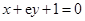 垂直,求
垂直,求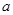 的值;
的值;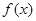 的单调区间;
的单调区间; ,当
,当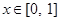 时,都有
时,都有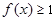 成立,求实数
成立,求实数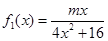 ,
,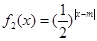 ,其中m∈R.
,其中m∈R.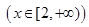 的单调性,并证明你的结论;
的单调性,并证明你的结论;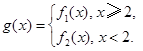 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围. (单位:千克)与销售价格
(单位:千克)与销售价格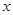 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式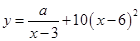 ,其中
,其中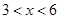 ,
,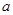 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克. 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.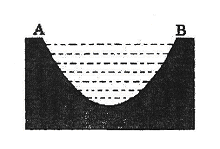
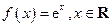 .
.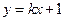 与
与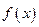 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值;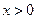 ,讨论曲线
,讨论曲线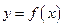 与曲线
与曲线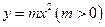 公共点的个数;
公共点的个数;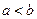 ,比较
,比较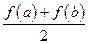 与
与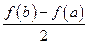 的大小,并说明理由.
的大小,并说明理由.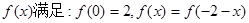 ,它的导函数的图象与直线
,它的导函数的图象与直线 平行.
平行. 的解析式;
的解析式; 的图象与直线
的图象与直线 有三个公共点,求m的取值范围.
有三个公共点,求m的取值范围.