题目内容
如图,在平面直角坐标系xOy中,椭圆C: =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为 ,点M的横坐标为
,点M的横坐标为 .
.

(1)求椭圆C的标准方程;
(2)设直线PA的斜率为k1,直线MA的斜率为k2,求k1·k2的取值范围.
 =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为 ,点M的横坐标为
,点M的横坐标为 .
.
(1)求椭圆C的标准方程;
(2)设直线PA的斜率为k1,直线MA的斜率为k2,求k1·k2的取值范围.
(1)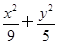 =1(2)
=1(2)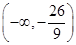
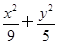 =1(2)
=1(2)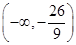
(1)由已知,得 解得
解得 ∴
∴ ∴椭圆C的标准方程为
∴椭圆C的标准方程为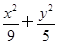 =1.
=1.
(2)设点P(x1,y1)(-2<x1<3),点M .∵点F、P、M三点共线,x1≠-2,
.∵点F、P、M三点共线,x1≠-2,
∴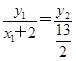 ,y2=
,y2= ,∴点M
,∴点M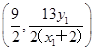 .
.
∵k1=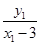 ,k2=
,k2= ,∴k1·k2=
,∴k1·k2=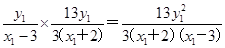 .
.
∵点P在椭圆C上,∴ =1,∴
=1,∴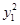 =-
=- (
( -9).
-9).
∴k1·k2=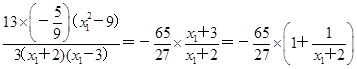 .
.
∵-2<x1<3,∴k1·k2<-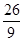 .∴k1·k2的取值范围是
.∴k1·k2的取值范围是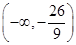
 解得
解得 ∴
∴ ∴椭圆C的标准方程为
∴椭圆C的标准方程为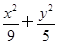 =1.
=1.(2)设点P(x1,y1)(-2<x1<3),点M
 .∵点F、P、M三点共线,x1≠-2,
.∵点F、P、M三点共线,x1≠-2,∴
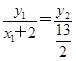 ,y2=
,y2= ,∴点M
,∴点M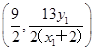 .
.∵k1=
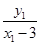 ,k2=
,k2= ,∴k1·k2=
,∴k1·k2=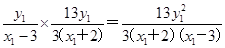 .
.∵点P在椭圆C上,∴
 =1,∴
=1,∴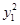 =-
=- (
( -9).
-9).∴k1·k2=
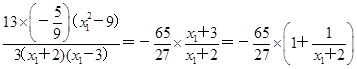 .
.∵-2<x1<3,∴k1·k2<-
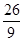 .∴k1·k2的取值范围是
.∴k1·k2的取值范围是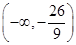

练习册系列答案
相关题目
 的两焦点在
的两焦点在 轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形
轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形 的动直线
的动直线 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q?若存在求出点Q的坐标;若不存在,请说明理由
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q?若存在求出点Q的坐标;若不存在,请说明理由  =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且 =λ
=λ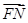 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0). ⊥
⊥ ;
; ·
· =
= ,求椭圆C的方程..
,求椭圆C的方程..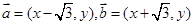 ,且
,且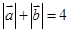 .
.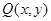 的轨迹
的轨迹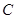 的方程;
的方程;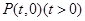 ,若斜率为
,若斜率为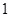 的直线
的直线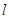 过点
过点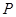 并与轨迹
并与轨迹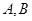 ,且对于轨迹
,且对于轨迹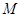 ,都存在
,都存在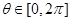 ,使得
,使得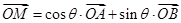 成立,试求出满足条件的实数
成立,试求出满足条件的实数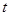 的值.
的值. 与
与 的曲线大致是( )
的曲线大致是( )
 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值. +
+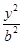 =1(a>b>0)与双曲线C2:x2-
=1(a>b>0)与双曲线C2:x2-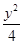 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )

 =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ .若△PF1F2的面积为9,则b=________.
.若△PF1F2的面积为9,则b=________.