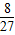题目内容
一个口袋中,有红、黑、白球各一个,从中任取一个球后,再放回进行第二次抽取,这样连续抽了3次,记3次抽取球颜色不全相同的概率为P1,3次抽取球颜色全不同的概率为P2,3次抽取球全无红色的概率为P3,则( )
A、P1=
| ||||||
B、P1=
| ||||||
C、P1=
| ||||||
D、P1=
|
分析:有放回的任取一个球,连续抽3次,3次抽取球颜色不全相同的对立事件是三次抽取的都相同,用对立事件公式来解题,其余两种事件的概率没有困难,同学们能选出正确结果.
解答:解:P1=1-3•
•
•
=
,
P2=
=
,
P3=
=
.
故选A
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 9 |
P2=
| ||||
| 3×3×3 |
| 2 |
| 9 |
P3=
| ||||||
| 3×3×3 |
| 8 |
| 27 |
故选A
点评:学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题.

练习册系列答案
相关题目
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=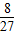
 P2=
P2=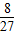 P3=
P3=
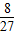 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=