题目内容
已知
=(a,-2),
=(1,1-a),且
∥
,则a=( )
| m |
| n |
| m |
| n |
| A、-1 | B、2或-1 | C、2 | D、-2 |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:根据两向量平行的坐标表示,列出方程,求出a的值即可.
解答:
解:∵
=(a,-2),
=(1,1-a),且
∥
,
∴a(1-a)-(-2)×1=0,
化简得a2-a-2=0,
解得a=2或a=-1;
∴a的值是2或-1.
故选:B.
| m |
| n |
| m |
| n |
∴a(1-a)-(-2)×1=0,
化简得a2-a-2=0,
解得a=2或a=-1;
∴a的值是2或-1.
故选:B.
点评:本题考查了平面向量平行的坐标表示的应用问题,是基础题目.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
直线(2m2-5m-3)x-(m2-9)y+4=0的倾斜角为
,则m的值是( )
| π |
| 4 |
| A、3 | B、2 | C、-2 | D、2与3 |
下列对应f:A→B是从集合 A到集合 B的函数的是( )
A、A={x|x>0},B={y|y≥0},f:y=
| ||
| B、A={x|x≥0},B={y|y>0},f:y=x2 | ||
| C、A={x|x是三角形},B={y|y是圆},f:每一个三角形对应它的内切圆 | ||
| D、A={x|x是圆},B={y|y是三角形},f:每一个圆对应它的外切三角形 |
不等式|x|>3的解集为( )
| A、{x|x>3} |
| B、{x|x>±3} |
| C、{x|-3<x<3} |
| D、{x|x<-3或x>3} |
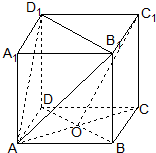 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.