题目内容
(12分)在梯形ABCD中AB∥CD,AD=DC=CB=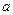 ,
, ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=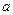 .
.
(1)求证:BC⊥平面ACFE;
(2)求EC与平面BEF所成角的正弦值.
.(1) ∵AB∥CD,AD=DC=CB=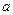 ,
,
∴梯形ABCD为等腰梯形,AB=2 .
.
三角形ACB中,∠ABC=60°,CB=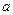 ,AB=2
,AB=2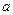
∴ AC= ,∠ACB=90°即BC⊥AC .................3分
,∠ACB=90°即BC⊥AC .................3分
又∵平面ACFE⊥平面ABCD,
平面ACFE∩平面ABCD=AC
∴ BC⊥平面ACFE. ..........................6分
(2)取B、F中点H,连结C、H.
∵BC⊥平面ACFE, EF 平面ACF
平面ACF E
E
∴BC⊥EF
又EF⊥FC , ∴EF⊥平面BCF
∵EF 平面BEF
平面BEF
∴平面BEF⊥平面BCF
又等腰△BCF中,CH⊥BF
∴CH⊥ 平面BEF,即∠CEH为所求角。……………9分
平面BEF,即∠CEH为所求角。……………9分
Rt△CHE中,CH= ,EC=2
,EC=2
sin∠CEH= . ..........................`12分
. ..........................`12分
解析

练习册系列答案
相关题目

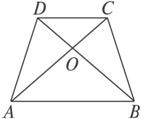
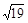 ,∠BAD=
,∠BAD= ,求梯形的高.
,求梯形的高.
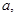
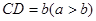 。若
。若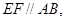 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为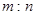 ,则可推算出:
,则可推算出: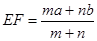 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设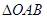 ,
,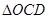 的面积分别为
的面积分别为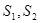 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为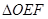 的面积
的面积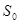 与
与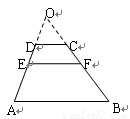
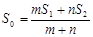 B.
B.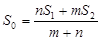
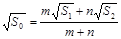 D.
D.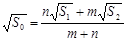
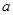 ,
,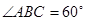 ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=