题目内容
【题目】设矩阵M＝
(其中a>0，b>0)．
(1)若a＝2，b＝3，求矩阵M的逆矩阵M－1；
(2)若曲线C：x2＋y2＝1在矩阵M所对应的线性变换作用下得到曲线C′：
＋y2＝1，求a，b的值．
【答案】（1）
（2）
【解析】(1)设矩阵M的逆矩阵M－1＝
，且M＝
.则MM－1＝
.
所以
＝.
所以2x1＝1,2y1＝0,3x2＝0,3y2＝1，即x1＝
，y1＝0，x2＝0，y2＝
，故所求的逆矩阵M－1＝.
(2)设曲线C上任意一点P(x，y)，它在矩阵M所对应的线性变换作用下得到点P′(x′，y′)，则
＝
，即
又点P′(x′，y′)在曲线C′上，所以
＋y′2＝1，则
＋b2y2＝1为曲线C的方程．又已知曲线C的方程为x2＋y2＝1，故
又a>0，b>0，所以
练习册系列答案
相关题目
【题目】为增强学生法治观念，营造“学宪法、知宪法、守宪法”的良好校园氛围，某学校开展了“宪法小卫士”活动，并组织全校学生进行法律知识竞赛.现从全校学生中随机抽取50人，统计他们的竞赛成绩，并得到如表所示的频数分布表.
分数段 |
|
|
|
|
|
人数 | 5 | 15 | 15 | 12 |
|
（Ⅰ）求频数分布表中的
的值，并估计这50名学生竞赛成绩的中位数（精确到0.1）；
（Ⅱ）将成绩在
内定义为“合格”，成绩在
内定义为“不合格”.请将列联表补充完整.
合格 | 不合格 | 合计 | |
高一新生 | 12 | ||
非高一新生 | 6 | ||
合计 |
试问：是否有95%的把握认为“法律知识的掌握合格情况”与“是否是高一新生”有关？说明你的理由；
（Ⅲ）在（Ⅱ）的前提下，在该50人中，按“合格与否”进行分层抽样，随机抽取5人，再从这5人中随机抽取2人，求恰好2人都合格的概率.
附：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
，
.
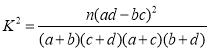