题目内容
半圆的直径AB=4，O为圆心，C是半圆上不同于A、B的任意一点，若P为半径OC的中点，则(
+
)•
的值是（ ）
| PA |
| PB |
| PC |
| A、、-2 |
| B、、-1 |
| C、、2 |
| D、、无法确定，与C点位置有关 |
分析：先利用O为AB的中点，且P为半径OC的中点，把（
+
）•
转化为2
•
=-2
2即可求出结论．
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
解答：解：∵O为AB的中点，且P为半径OC的中点
∴
+
=2
，
=-
∴（
+
）•
=2
•
=-2
2=-2×(
)2=-2×1=-2．
故选：A
∴
| PA |
| PB |
| PO |
| PO |
| PC |
∴（
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| |OC| |
| 2 |
故选：A
点评：本题主要考查平面向量数量积的运算以及三角形中线向量所具有的性质，是对基础知识的考查，属于基础题．本题的关键在于利用三角形的中线把
+
转化为2
．
| PA |
| PB |
| PO |
练习册系列答案
活力课时同步练习册系列答案
相关题目
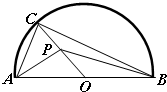如图，半圆的直径AB=4，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则
如图，半圆的直径AB=4，O为圆心，C是半圆上与A、B不同的任意一点，P是半径OC上的动点，则