题目内容
半圆的直径AB=4，O为圆心，C是半圆上不同于A，B的任意一点，若P为半径OC上的动点，则(
+
)•
的最小值是
| PA |
| PB |
| PC |
-2
-2
．分析：由题意可得
+
=2
，要求的式子即 2
•
=-2|
|•|
|．再根据|
|+|
|=|
|=2为定值，利用基本不等式求得-2|
|•|
|的最小值．
| PA |
| PB |
| PO |
| PO |
| PC |
| PO |
| PC |
| PO |
| PC |
| OC |
| PO |
| PC |
解答：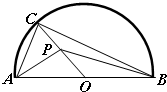
解：因为O为AB的中点，所以
+
=2
，
从而 (
+
)•
=2
•
=-2|
|•|
|．
又|
|+|
|=|
|=2为定值，再根据|
|•|
|≤(
)2=1，
可得-2|
|•|
|≥-2，
所以当且仅当|
|=|
|=1时，即P为OC的中点时，等号成立，
(
+
)•
取得最小值是-2，
故答案为-2．
解：因为O为AB的中点，所以| PA |
| PB |
| PO |
从而 (
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| PC |
又|
| PO |
| PC |
| OC |
| PO |
| PC |
|
| ||||
| 2 |
可得-2|
| PO |
| PC |
所以当且仅当|
| PO |
| PC |
(
| PA |
| PB |
| PC |
故答案为-2．
点评：本题主要考查向量在几何中的应用，两个向量的数量积公式的应用，属于中档题．
练习册系列答案
相关题目
半圆的直径AB=4，O为圆心，C是半圆上不同于A、B的任意一点，若P为半径OC的中点，则(
+
)•
的值是（ ）
| PA |
| PB |
| PC |
| A、、-2 |
| B、、-1 |
| C、、2 |
| D、、无法确定，与C点位置有关 |
如图，半圆的直径AB=4，O为圆心，C是半圆上与A、B不同的任意一点，P是半径OC上的动点，则