题目内容
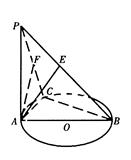
(14分)如图,已知四棱锥 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
(1)求证:SA⊥平面ABCD
(2)求证:NF∥平面SAD;
(3)求二面角A-BN-C的余弦值.

 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.(1)求证:SA⊥平面ABCD
(2)求证:NF∥平面SAD;
(3)求二面角A-BN-C的余弦值.

17. (1)∵ ∴
∴ -------(3分)
-------(3分)
(2)取SD的中点N,连接MN,AM
∵N为SC的中点,∴MN∥CD且MN=
又矩形ABCD中,F为AB的中点,∴AF∥CD且AF=
∴AF∥MN且AF="MN " 则四边形AFNM为平行四边形----------(5分)
∴AM∥FN AM 平面SAD FN
平面SAD FN 平面SAD ∴NF∥平面SAD------(7分)
平面SAD ∴NF∥平面SAD------(7分)
(3)以 点为原点,
点为原点, 所在直线为
所在直线为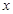 轴,
轴, 所在直线为
所在直线为 轴,SA所在直线为
轴,SA所在直线为 轴的空间直角坐标系,如图所示.
轴的空间直角坐标系,如图所示.

则依题意可知相关各点的坐标分别是:
 ,
, ,
, ,
, ,
, 如下图所示.
如下图所示.
∴ ------------------…(9分)
------------------…(9分)
∴ ,
,
 --------------(10分)
--------------(10分)
设平面ABN的法向量

令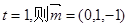 ----------------------------------------(11分)
----------------------------------------(11分)
设平面 的法向量
的法向量 ,则
,则 ,
,
所以 即
即
所以
令 ,则
,则 ------------------------------ (12分)
------------------------------ (12分)
∴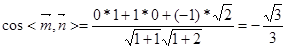 ------------ (13分)
------------ (13分)
由图形知,二面角 是钝角二面角
是钝角二面角
所以二面角 的余弦值为
的余弦值为 ......................................................... (14分)
......................................................... (14分)
 ∴
∴ -------(3分)
-------(3分)(2)取SD的中点N,连接MN,AM
∵N为SC的中点,∴MN∥CD且MN=

又矩形ABCD中,F为AB的中点,∴AF∥CD且AF=

∴AF∥MN且AF="MN " 则四边形AFNM为平行四边形----------(5分)
∴AM∥FN AM
 平面SAD FN
平面SAD FN 平面SAD ∴NF∥平面SAD------(7分)
平面SAD ∴NF∥平面SAD------(7分)(3)以
 点为原点,
点为原点, 所在直线为
所在直线为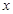 轴,
轴, 所在直线为
所在直线为 轴,SA所在直线为
轴,SA所在直线为 轴的空间直角坐标系,如图所示.
轴的空间直角坐标系,如图所示.
则依题意可知相关各点的坐标分别是:
 ,
, ,
, ,
, ,
, 如下图所示.
如下图所示.∴
 ------------------…(9分)
------------------…(9分)∴
 ,
,
 --------------(10分)
--------------(10分)设平面ABN的法向量


令
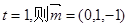 ----------------------------------------(11分)
----------------------------------------(11分)设平面
 的法向量
的法向量 ,则
,则 ,
,所以
 即
即
所以

令
 ,则
,则 ------------------------------ (12分)
------------------------------ (12分)∴
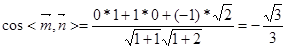 ------------ (13分)
------------ (13分)由图形知,二面角
 是钝角二面角
是钝角二面角所以二面角
 的余弦值为
的余弦值为 ......................................................... (14分)
......................................................... (14分)略

练习册系列答案
相关题目
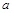 ,
,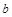 ,
,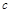 中,若
中,若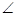 ABC=60
ABC=60 ,E
,E C
C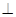 面ABCD,FA
面ABCD,FA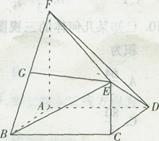
 中,四边形
中,四边形 为平行四边形,且面
为平行四边形,且面 面
面 ,
,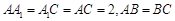 ,且
,且 ,
, 为
为 中点.
中点. 平面
平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.
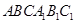 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形, ,
, 平面
平面 .
. 是
是 的中点,求证:
的中点,求证:
 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
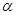 和直线
和直线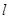 ,
,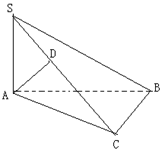
 是异面直线,
是异面直线, 求证:AD与BC是异面直线。
求证:AD与BC是异面直线。 是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面
是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面 于E,
于E,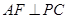 于F,因此________⊥平面PBC(请填图上的一条直线)
于F,因此________⊥平面PBC(请填图上的一条直线)