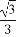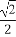如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=,点E为AB上的动点,则D1E+CE的最小值为( )(A)2 (B)(C)+1 (D)2+ 题目和参考答案——青夏教育精英家教网——

题目内容

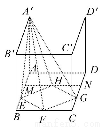
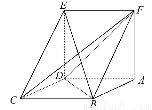
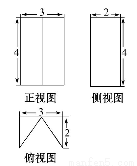
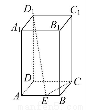
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=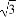,点E为AB上的动点,则D1E+CE的最小值为(　　)

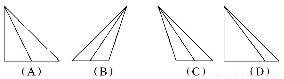
(A)2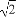 (B)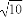

(C)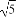+1 (D)2+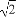

B

【解析】将正方形ABCD沿AB向下翻折到对角面ABC1D1内成为正方形ABC2D2,在矩形C1D1D2C2中连接D1C2,与AB的交点即为所求最小值点E,此时D1E+CE=D1C2.因为对角线BC1=2,C1C2=3,故D1C2===.

练习册系列答案

中考试题研究满分特训方案系列答案

中考总复习名师A计划系列答案

百题大过关系列答案

考向标初中毕业学业考试指导系列答案

初中复习指导系列答案

发现中考系列答案

高考总复习优化方案系列答案

山西新中考系列答案

中考精确制导系列答案

中考一路领航系列答案

相关题目

已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有(　　)

(A)0个 (B)1个 (C)2个 (D)3个

如图,正方体ABCD-A'B'C'D'中,M,E是AB的三等分点,G,N是CD的三等分点,F,H分别是BC,MN的中点,则四棱锥A'-EFGH的侧视图为( )

在正方体ABCD-A1B1C1D1中,二面角A1-BD-C1的余弦值为(　　)

(A) (B) (C) (D)

如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.记CD=x,V(x)表示四棱锥F-ABCD的体积.

(1)求V(x)的表达式.

(2)求V(x)的最大值.

某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是(　　)

(A)16 (B)12 (C)8 (D)6

已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共面,则实数λ=　　　.

已知f(n)=1+++…+(n∈N*),用数学归纳法证明f(2n)>时,f(2k+1)-f(2k)等于　　　.

已知函数f(x)=x3-x2+x+b,其中a,b∈R.

(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=5x-4,求函数f(x)的解析式.

(2)当a>0时,讨论函数f(x)的单调性.