题目内容
(1)已知sinx+sin2x=1,求cos2x+cos4x的值;
(2)已知在△ABC中,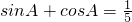
①求sinAcosA;
②判断△ABC是锐角三角形还是钝角三角形;
③求tanA的值.
解:(1)∵已知sinx+sin2x=1,∴sinx=cos2x,∴cos2x+cos4x=sinx+sin2x=1.
(2)∵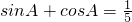 ,平方可得 1+2sinA cosA=
,平方可得 1+2sinA cosA= ,∴sinA cosA=-
,∴sinA cosA=- .
.
又 0<A<π,可得A为钝角,cosA<0,sinA>0,且|sinA|>|cosA|.
再由 sin2A+cos2A=1,可得cosA=- ,sinA=
,sinA= .
.
故 tanA= =
= =-
=- .
.
分析:(1)由已知的等式可得sinx=cos2x,代入要求的式子化简可得cos2x+cos4x=sinx+sin2x.
(2)根据题意,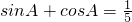 ,平方可得sinAcosA 的值,再根据sinA和cosA 平方和等于1,求出sinA和cosA 的值,从而判断△ABC的形状,利用同角三角函数的基本关系求得tanA的值.
,平方可得sinAcosA 的值,再根据sinA和cosA 平方和等于1,求出sinA和cosA 的值,从而判断△ABC的形状,利用同角三角函数的基本关系求得tanA的值.
点评:本题考查同角三角函数的基本关系的应用,诱导公式的应用,求出sinA和cosA的值,是解题的关键.
(2)∵
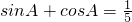 ,平方可得 1+2sinA cosA=
,平方可得 1+2sinA cosA= ,∴sinA cosA=-
,∴sinA cosA=- .
.又 0<A<π,可得A为钝角,cosA<0,sinA>0,且|sinA|>|cosA|.
再由 sin2A+cos2A=1,可得cosA=-
 ,sinA=
,sinA= .
.故 tanA=
 =
= =-
=- .
.分析:(1)由已知的等式可得sinx=cos2x,代入要求的式子化简可得cos2x+cos4x=sinx+sin2x.
(2)根据题意,
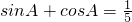 ,平方可得sinAcosA 的值,再根据sinA和cosA 平方和等于1,求出sinA和cosA 的值,从而判断△ABC的形状,利用同角三角函数的基本关系求得tanA的值.
,平方可得sinAcosA 的值,再根据sinA和cosA 平方和等于1,求出sinA和cosA 的值,从而判断△ABC的形状,利用同角三角函数的基本关系求得tanA的值.点评:本题考查同角三角函数的基本关系的应用,诱导公式的应用,求出sinA和cosA的值,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目