题目内容
设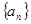 为等差数列,
为等差数列,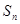 是等差数列的前
是等差数列的前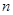 项和,已知
项和,已知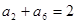 ,
,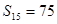 .
.
(1)求数列的通项公式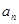 ;
;
(2)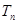 为数列
为数列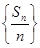 的前
的前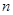 项和,求
项和,求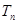 .
.
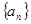 为等差数列,
为等差数列,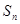 是等差数列的前
是等差数列的前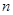 项和,已知
项和,已知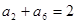 ,
,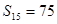 .
.(1)求数列的通项公式
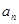 ;
;(2)
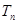 为数列
为数列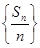 的前
的前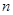 项和,求
项和,求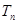 .
.(1)n-3(2)

本试题主要是考查了数列的通项公式的求解和数列求和的综合运用。
(1)因为等差数列的定义可知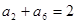 ,
,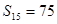 ,得到方程组,得到首项而后公差,解得。
,得到方程组,得到首项而后公差,解得。
(2)利用数列的前n项和的关系式,那么可知 ,然后利用性质得到结论。
,然后利用性质得到结论。
解:(1)设 ,由题意可得
,由题意可得


(2)

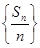 是等差数列,首项是0,公差为
是等差数列,首项是0,公差为

(1)因为等差数列的定义可知
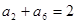 ,
,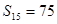 ,得到方程组,得到首项而后公差,解得。
,得到方程组,得到首项而后公差,解得。(2)利用数列的前n项和的关系式,那么可知
 ,然后利用性质得到结论。
,然后利用性质得到结论。解:(1)设
 ,由题意可得
,由题意可得

(2)


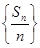 是等差数列,首项是0,公差为
是等差数列,首项是0,公差为


练习册系列答案
相关题目
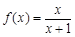 , 若数列
, 若数列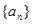 (n∈N*)满足:
(n∈N*)满足: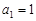 ,
,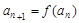
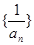 为等差数列,并求数列
为等差数列,并求数列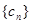 满足:
满足: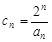 ,求数列
,求数列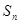 .
.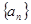 的各项都为正数,其前
的各项都为正数,其前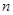 项和为
项和为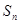 ,已知对任意
,已知对任意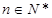 ,
,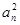 和
和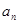 的等差中项.
的等差中项.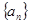 的通项公式;
的通项公式;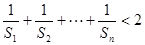 .
.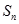 为数列
为数列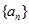 的前
的前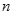 项和,对任意的
项和,对任意的 ,都有
,都有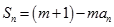
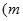 为常数,且
为常数,且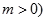 .
.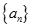 是等比数列;
是等比数列;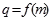 ,数列
,数列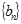 满足
满足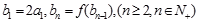 ,求数列
,求数列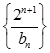 的前
的前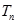 .
. 中,若
中,若 ,则
,则 的值为( )
的值为( ) B
B  C
C  D
D 
 的前
的前 项和为
项和为 ,已知
,已知 ,
, 和公差
和公差 的值;
的值; ,求
,求 的前
的前 项和记为
项和记为 ,已知
,已知 .
. ;
; ,求数列
,求数列 的前
的前 .
.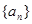 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第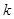 个1和第
个1和第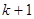 个1之间有
个1之间有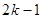 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前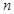 项的和为
项的和为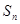 .
.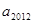 和
和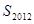 ;
;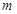 ,使得
,使得 ?如果存在,求出
?如果存在,求出