题目内容
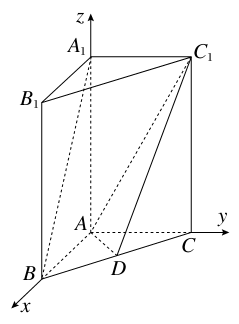
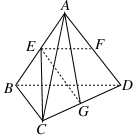
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
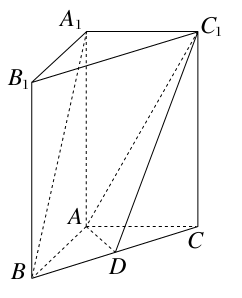
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.

(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
(1) (2)
(2)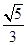
 (2)
(2)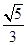
解:(1)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4),∴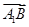 =(2,0,-4),
=(2,0,-4), =(1,-1,-4).
=(1,-1,-4).
∵cos〈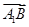 ,
,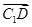 〉=
〉=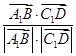 =
=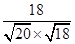 =
= ,
,
∴异面直线A1B与C1D所成角的余弦值为 .
.
(2)设平面ADC1的法向量为n1=(x,y,z),∵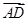 =(1,1,0),
=(1,1,0),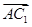 =(0,2,4),∴n1·
=(0,2,4),∴n1·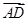 =0,n1·
=0,n1·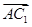 =0,即x+y=0且2y+4z=0,取z=1,得x=2,y=-2,∴n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.
=0,即x+y=0且2y+4z=0,取z=1,得x=2,y=-2,∴n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.
由cosθ=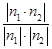 =
=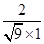 =
=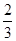 ,得sinθ=
,得sinθ=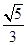 .
.
因此,平面ADC1与平面ABA1夹角的正弦值为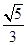 .
.
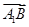 =(2,0,-4),
=(2,0,-4),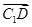 =(1,-1,-4).
=(1,-1,-4).
∵cos〈
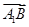 ,
,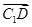 〉=
〉=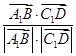 =
=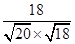 =
= ,
,∴异面直线A1B与C1D所成角的余弦值为
 .
.(2)设平面ADC1的法向量为n1=(x,y,z),∵
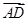 =(1,1,0),
=(1,1,0),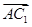 =(0,2,4),∴n1·
=(0,2,4),∴n1·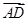 =0,n1·
=0,n1·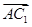 =0,即x+y=0且2y+4z=0,取z=1,得x=2,y=-2,∴n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.
=0,即x+y=0且2y+4z=0,取z=1,得x=2,y=-2,∴n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.由cosθ=
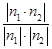 =
=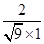 =
=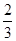 ,得sinθ=
,得sinθ=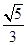 .
.因此,平面ADC1与平面ABA1夹角的正弦值为
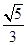 .
.
练习册系列答案
相关题目
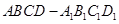 的所有棱长都相等,
的所有棱长都相等,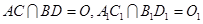 ,四边形
,四边形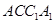 和四边形
和四边形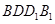 为矩形.
为矩形.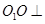 底面
底面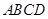 ;
; ,求二面角
,求二面角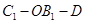 的余弦值.
的余弦值.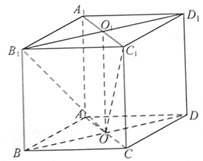
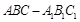 中,
中,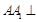 底面
底面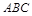 ,
,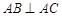 ,
,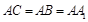 ,
,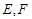 分别是棱
分别是棱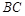 ,
,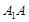 的中点,
的中点,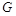 为棱
为棱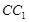 上的一点,且
上的一点,且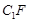 //平面
//平面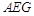 .
.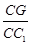 的值;
的值;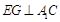 ;
;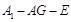 的余弦值.
的余弦值.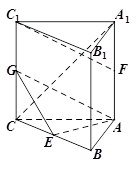
 ,
, (a > 0)(1)求a的值,使点M(
(a > 0)(1)求a的值,使点M( ,
,  )到直线
)到直线 的最短距离为
的最短距离为 ;(2)若不等式
;(2)若不等式 在
在 [1,4]恒成立,求a的取值范围.
[1,4]恒成立,求a的取值范围.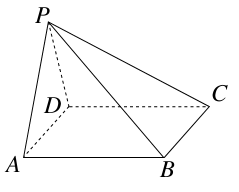
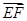 ·
·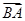 ;
;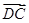 ;
;