题目内容
已知f(x)＝logax(a>0且a≠1)，如果对于任意的x∈
都有|f(x)|≤1成立，试求a的取值范围．
都有|f(x)|≤1成立，试求a的取值范围．解：当a>1时，f(x)＝logax在上单调递增，要使x∈都有|f(x)|≤1成立，则有
解得a≥3.
∴此时a的取值范围是a≥3.
当0<a<1时，f(x)＝logax在上单调递减，
要使x∈都有|f(x)|≤1成立，则有
，解得0<a≤
.
∴此时，a的取值范围是0<a≤.
综上可知，a的取值范围是
∪[3，＋∞)．
上单调递增，要使x∈都有|f(x)|≤1成立，则有解得a≥3.∴此时a的取值范围是a≥3.
当0<a<1时，f(x)＝logax在
上单调递减，要使x∈
都有|f(x)|≤1成立，则有，解得0<a≤.∴此时，a的取值范围是0<a≤
.综上可知，a的取值范围是
∪[3，＋∞)．
练习册系列答案
相关题目
，若f(m)<f(－m)，则实数m的取值范围是____________．
，b=
，c=log3
，则a，b，c的大小关系是（ ）
”：
，
、
.对任意实数
、
、
，
；②
；③
.
.
的定义域为 ．
．
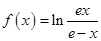，则
=_______________。