Question

【题目】已知圆，圆，动圆与圆外切并与圆内切，圆心的轨迹为曲线.

（1）求的方程；

（2）是与圆，圆都相切的一条直线，与曲线交于两点，当圆的半径最长时，求.

Answer 1

【答案】(1) ；(2) 或.

【解析】

试题分析：对于（1），圆的圆心为，半径，圆的圆心为，半径，设圆的圆心为，半径为，由已知条件不难得到，进而可得曲线是以为左、右焦点，长半轴长为，短半轴长为的椭圆，据此即可求出其方程；对于（2），首先根据已知条件圆的方程，接下来需要分直线的斜率存在与不存在两种情况，并结合点到直线的距离公式和弦长公式进行解答即可.

试题解析：由已知得圆的圆心为，半径；圆的圆心为，半径，设圆的圆心为，半径为.

（1）因为圆与圆外切并且与圆内切，所以

.

由椭圆的定义可知，曲线是以为左、右焦点，长半轴长为，短半轴长为的椭圆（左顶点除外），其方程为.……5分

（2）对于曲线上任意一点，由于，所以，当且仅当圆的圆心为时，.所以当圆的半径最长时，其方程为

.

若的倾斜角为，则与轴重合，可得.

若的倾斜角不为，由知不平行于轴，设与轴的交点为，

则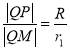，可求得，所以可设.由与圆相切得，解得.

当时，将带入，并整理得，

解得.所以.

当时，由图形的对称性可知.综上，或.……12分