题目内容
已知集合A={x|2x-1>0},B={x|m-1<x<2m+1}设全集∪=R
(1)若m=1,求(∁∪A)∩B
(2)若B∩A=B,求实数m的取值范围.
(1)若m=1,求(∁∪A)∩B
(2)若B∩A=B,求实数m的取值范围.
考点:交、并、补集的混合运算,集合的包含关系判断及应用
专题:集合
分析:(1)将m=1代入集合B中的不等式确定出B,求出A中不等式的解集确定出A,根据全集U=R求出A的补集,找出A补集与B的交集即可;
(2)根据B与A的交集为B,得到B为A的子集,即可确定出m的范围.
(2)根据B与A的交集为B,得到B为A的子集,即可确定出m的范围.
解答:
解:(1)由A中不等式解得:x>
,即A=(
,+∞),
∵全集U=R,∴∁∪A=(-∞,
],
将m=1代入集合B中得:0<x<3,即B=(0,3),
则(∁∪A)∩B=(0,
];
(2)∵B∩A=B,∴B⊆A,
当B=∅时,则有m-1≥2m+1,即m≤-2,满足题意;
当B≠∅时,则有m-1<2m+1,即m>-2,
∵A=(
,+∞),B=(m-1,2m+1),
∴m-1≥
,
解得:m≥
,
综上,实数m的范围为(-∞,-2]∪[
,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
∵全集U=R,∴∁∪A=(-∞,
| 1 |
| 2 |
将m=1代入集合B中得:0<x<3,即B=(0,3),
则(∁∪A)∩B=(0,
| 1 |
| 2 |
(2)∵B∩A=B,∴B⊆A,
当B=∅时,则有m-1≥2m+1,即m≤-2,满足题意;
当B≠∅时,则有m-1<2m+1,即m>-2,
∵A=(
| 1 |
| 2 |
∴m-1≥
| 1 |
| 2 |
解得:m≥
| 3 |
| 2 |
综上,实数m的范围为(-∞,-2]∪[
| 3 |
| 2 |
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某圆台的正视图是上底与腰长均为2,下底边为4的等腰梯形,则此圆台的表面积为( )
| A、10π | B、11π |
| C、12π | D、13π |
 直三棱柱ABC-A1B1C1,棱AA1上有一个动点E满足AE=λA1E.
直三棱柱ABC-A1B1C1,棱AA1上有一个动点E满足AE=λA1E.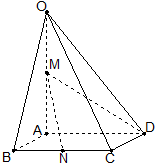 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC= 三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC.
三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC.