题目内容
“a>b>0”是“a2>b2”的( ) 条件.
| A、充分不必要 | B、必要不充分 | C、充要 | D、既不充分也不必要 |
分析:结合不等式的解法,利用充分条件和必要条件的定义进行判断即可.
解答:解:当a>b>0时,a2>b2成立.
当a=-2,b=0时,满足a2>b2,但a>b>0不成立,
∴“a>b>0”是“a2>b2”的充分不必要条件.
故选:A.
当a=-2,b=0时,满足a2>b2,但a>b>0不成立,
∴“a>b>0”是“a2>b2”的充分不必要条件.
故选:A.
点评:主要是考查了充分条件的判定的运用,利用不等式的性质是解决本题的关键.

练习册系列答案
相关题目
0<a<1,下列不等式一定成立的是( )
| A、|log(1+a)(1-a)|+|log(1-a)(1+a)|>2; | B、|log(1+a)(1-a)|<|log(1-a)(1+a)|; | C、|log(1+a)(1-a)+log(1-a)(1+a)|<|log(1+a)(1-a)|+|log(1-a)(1+a)|; | D、|log(1+a)(1-a)-log(1-a)(1+a)|>|log(1+a)(1-a)|-|log(1-a)(1+a)| |

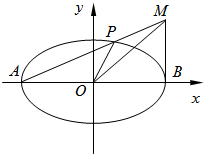 如图,已知椭圆
如图,已知椭圆 ﹣a﹣b,那么
﹣a﹣b,那么