题目内容

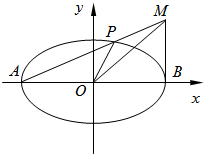精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，A、B是长轴的左、右端点，动点M满足MB⊥AB，联结AM，交椭圆于点P．
（1）当a=2，b=
2
时，设M（2，2），求
OP
•
OM
的值；
（2）若
OP
•
OM
为常数，探究a、b满足的条件？并说明理由；
（3）直接写出
OP
•
OM
为常数的一个不同于（2）结论类型的几何条件．
分析：（1）利用点斜式可得AM的方程，与椭圆的方程联立可得点P，利用数量积可得
OP
•
OM
；
（2）设P（x0，y0），M（a，t）（t≠0），利用A、P、M三点共线，可得
y0
x0+a
=
t
2a
，即t=
2ay0
x0+a
．利用
x02
a2
+
y02
b2
=1，可得y02=
b2(a-x0)(a+x0)
a2
．于是
OP
•
OM
=2b2+
a2-2b2
a
x0．令a2-2b2=0即可．
（3）利用（2）中的：a2=2b2即可给出：“设F1为椭圆的焦点，C为短轴的顶点，当△COF1为等腰三角形时，
OP
•
OM
为常数2b2或a2．”或给出“当PB⊥OM时，
OP
•
OM
为常数2b2或a2．”
解答：解 （1）直线AM：y=
1
2
(x+2)，
与椭圆的方程联立
y=
1
2
(x+2)
x2
4
+
y2
2
=1
，解得P(
2
3
，
4
3
)．
∴
OP
•
OM
=(
2
3
，
4
3
)•(2，2)=4．     
（2）设P（x0，y0），M（a，t）（t≠0），
∵A、P、M三点共线，于是
y0
x0+a
=
t
2a
，即t=
2ay0
x0+a
．   
又
x02
a2
+
y02
b2
=1，即y02=
b2(a-x0)(a+x0)
a2
．        
∴
OP
•
OM
=ax0+ty0=ax0+
2ay02
x0+a
=ax0+
2b2(a-x0)
a
=2b2+
a2-2b2
a
x0．
∴当a2-2b2=0时，
OP
•
OM
为常数2b2． 
（3）给出“设F1为椭圆的焦点，C为短轴的顶点，当△COF1为等腰三角形时，
OP
•
OM
为常数2b2或a2．”
或给出“当PB⊥OM时，
OP
•
OM
为常数2b2或a2．”
点评：本题考查了直线与椭圆相交问题转化为方程联立、数量积运算、三点共线问题与直线斜率的关系、探究性问题等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
如图，已知椭圆C：
x2
a2
+
y2
b2
=1的离心率为
3
2
，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．
（Ⅰ）求椭圆C的方程：
（Ⅱ）若S△PMN=
3
2
，求直线AB的方程．
如图，已知椭圆C：
x2
36
+
y2
20
=1的左顶点，右焦点分别为A，F，右准线为l，N为l上一点，且在x轴上方，AN与椭圆交于点M．
（1）若AM=MN，求证：AM⊥MF；
（2）过A，F，N三点的圆与y轴交于P，Q两点，求PQ的最小值．
（2012•深圳一模）如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，以椭圆C的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0），设圆T与椭圆C交于点M与点N．
（1）求椭圆C的方程；
（2）求
TM
•
TN
的最小值，并求此时圆T的方程；
（3）设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：|OR|•|OS|为定值．
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左顶点，右焦点分别为A、F，右准线为m．圆D：x2+y2+x-3y-2=0．
（1）若圆D过A、F两点，求椭圆C的方程；
（2）若直线m上不存在点Q，使△AFQ为等腰三角形，求椭圆离心率的取值范围．
（3）在（1）的条件下，若直线m与x轴的交点为K，将直线l绕K顺时针旋转
π
4
得直线l，动点P在直线l上，过P作圆D的两条切线，切点分别为M、N，求弦长MN的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网