题目内容
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,点
,点![]() 是
是![]() 中点.
中点.
(Ⅰ)若![]() 为
为![]() 中点,证明:
中点,证明:![]() //平面
//平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 边上任一点,证明:
边上任一点,证明:![]() ;
;
(Ⅲ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
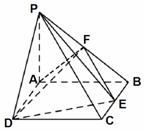 |
证明(I)E为BC中点,F为PB中点
∴EF∥CP CP![]() 平面PAC,
平面PAC,![]() 平面PAC
平面PAC
∴EF∥平面PAC
(II)∵PA⊥平面ABCD ∴PA⊥BC
又AB⊥BC
![]() ∴BC⊥平面PAB BC⊥AF
∴BC⊥平面PAB BC⊥AF
又PA=AB,F为PB中点,∴PB⊥AF
![]() ,AF⊥平面PBC ∴AF⊥PE
,AF⊥平面PBC ∴AF⊥PE
(III)分别以直线AD、DB、DP为x轴,y轴,z轴建立空间直角坐标系
P(0,0,1) ![]() B(0,1,0),
B(0,1,0), ![]()
![]()
![]()
设平面PDE的一个法向量为![]()
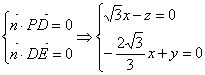
令x=1得平面PDE和一个法向量![]()
又![]() AP与平面PDE所成角为
AP与平面PDE所成角为![]()
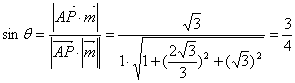
PA与平面PDE所成角正弦值为![]() .
.

练习册系列答案
相关题目
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD= 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.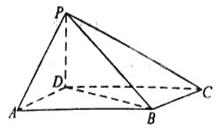
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,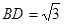 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,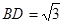 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。