Question

如图2-1-17,AM是⊙O的直径,过⊙O上一点B作BN⊥AM,垂足为N,其延长线交⊙O于点C,弦CD交AM于点E.

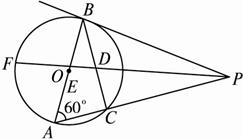
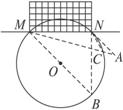
(1)如果CD⊥AB,求证:EN=MN.

(2)如果弦CD交AB于点F,且CD=AB,求证:CE²=EF·ED.

(3)如果弦CD、AB的延长线交于点F,且CD=AB,那么(2)的结论是否仍成立?若成立,请证明;若不成立,请说明理由.

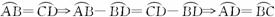
图2-1-17

Answer 1

(1)证明:连结BM,∵CD⊥AB,

∴∠BCE+∠ABC=90°.

∵AM是直径,∴∠MBN+∠ABC=90°.

∴∠BCE=∠MBN.

又∵ON⊥BC,∴BN=CN,∠BNM=∠CNE.

∴△BNM≌△CNE.

∴EN=MN.

(2)证明:连结BD、BE、AC.

∵CD=AB∠ACD=∠D.

△ABE≌△ACE∠ACD=∠ABE.

△BEF∽△DEB=

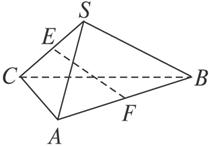
(3)如图2-1-18,(2)的结论仍成立.

图2-1-18

证明:∵AM⊥BC,

∴BE=CE,AB=AC.

∴∠1=∠2,∠3=∠4.

∵AB=CD,

∴∠4=∠DBC.

∴∠3=∠DBC=∠2+∠5.

又∵∠3=∠F+∠1,∴∠F=∠5.

∵∠BED=∠FEB,∴△BDE∽△FBE.

∴.

∴BE²=EF·ED.∴CE²=EF·ED.