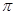题目内容
正方体 中,
中,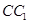 与平面
与平面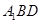 所成角的余弦值为( )
所成角的余弦值为( )
 中,
中,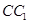 与平面
与平面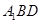 所成角的余弦值为( )
所成角的余弦值为( )A.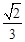 | B.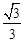 | C.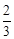 | D.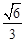 |
D
试题分析:根据题意,可以借助于体积法的得到点
 到平面的距离,因为
到平面的距离,因为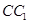 与平面
与平面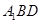 所成角,等于
所成角,等于 与平面
与平面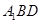 所成角,那么根据底面是等腰三角形,设正方体的边长为1,可知其面积为
所成角,那么根据底面是等腰三角形,设正方体的边长为1,可知其面积为 ,即根据
,即根据
而
 =1,则线面角的正弦值为
=1,则线面角的正弦值为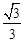 ,而其余弦值为
,而其余弦值为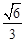 ,选D.
,选D.点评:解决线面角的求解,关键是作出角,利用平面的垂线,和斜线在平面内的射影,结合斜线段和斜线段在平面内的射影的夹角来得到结论,或者利用斜线段和垂线段的长度比值来得到。属于基础题。

练习册系列答案
相关题目



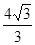


 ,则正三棱锥
,则正三棱锥 外接球的表面积为___________.
外接球的表面积为___________. 和直线
和直线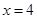 ,
,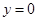 所围成的平面图形,绕
所围成的平面图形,绕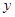 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为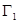 ;由同时满足
;由同时满足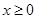 ,
,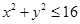 ,
,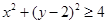 ,
,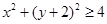 的点
的点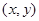 构成的平面图形,绕
构成的平面图形,绕 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察



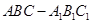 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若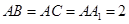 ,
,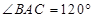 ,则此球的表面积等于 。
,则此球的表面积等于 。
 的球在一个圆锥内部,它的轴截面是一个正三角形与其内切圆,则圆锥的全面积与球面面积的比是 ( )
的球在一个圆锥内部,它的轴截面是一个正三角形与其内切圆,则圆锥的全面积与球面面积的比是 ( )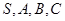 是球
是球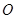 表面上的点,
表面上的点,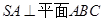 ,
,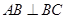 ,
,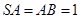 ,
,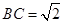 ,
,