题目内容
函数若f(x)=
,则f(x)的定义域是
| 1 | ||||
|
(-
,0)
| 1 |
| 2 |
(-
,0)
.| 1 |
| 2 |
分析:由函数的解析式可得 log
(2x+1)>0,化简可得 0<2x+1<1,由此求得f(x)的定义域.
| 1 |
| 2 |
解答:解:∵函数f(x)=
,
∴log
(2x+1)>0,
∴0<2x+1<1,解得-
<x<0,
故答案为 (-
,0).
| 1 | ||||
|
∴log
| 1 |
| 2 |
∴0<2x+1<1,解得-
| 1 |
| 2 |
故答案为 (-
| 1 |
| 2 |
点评:本题主要考查求函数的定义域,对数不等式的解法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 则f(
则f( ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0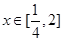 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t) 的最值
的最值