题目内容
已知函数 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的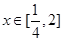 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t) 的最值
的最值
【答案】
答:①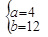 ;②t=
;②t=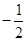 最小值
最小值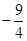 ,t=3最大值10。
,t=3最大值10。
【解析】
试题分析:答:①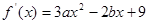 ,
,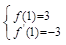
 ………2分
………2分
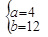 ………4分
………4分
②列表如下:
|
|
|
|
|
|
|
|
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
|
|
4 |
f(x)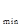 =2 8分
=2 8分
对任意的 都有f(x)
都有f(x)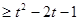 成立,
成立,
f(x)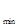 ="2"
="2" 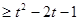 ,
, 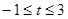 10分
10分
g(t)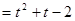 (
(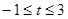 ),
),
t=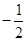 最小值
最小值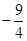 ,t=3最大值10 12分
,t=3最大值10 12分
考点:导数计算,利用导数研究函数的单调性、极值、最值,不等式恒成立问题。
点评:中档题,此类问题较为典型,是导数应用的基本问题。在某区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。求最值应遵循“求导数,求驻点,计算极值及端点函数值,比较确定最值”。不等式恒成立问题,往往通过构造函数,研究函数的最值,使问题得到解决。本题利用“表解法”,清晰、直观、易懂。

练习册系列答案
相关题目
















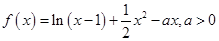 .
. 的最小值为f(t),求t的值。
的最小值为f(t),求t的值。