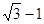题目内容
椭圆C的中心在原点O,它的短轴长为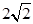 ,相应的焦点
,相应的焦点 的准线了l与x轴相交于A,|OF1|=2|F1A|.
的准线了l与x轴相交于A,|OF1|=2|F1A|.
(1)求椭圆的方程;
(2)过椭圆C的左焦点作一条与两坐标轴都不垂直的直线l,交椭圆于P、Q两点,若点M在 轴上,且使MF2为
轴上,且使MF2为 的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;
的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;
(3)根据(2)中的结论,猜测椭圆 的“左特征点”的位置.
的“左特征点”的位置.
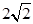 ,相应的焦点
,相应的焦点 的准线了l与x轴相交于A,|OF1|=2|F1A|.
的准线了l与x轴相交于A,|OF1|=2|F1A|.(1)求椭圆的方程;
(2)过椭圆C的左焦点作一条与两坐标轴都不垂直的直线l,交椭圆于P、Q两点,若点M在
 轴上,且使MF2为
轴上,且使MF2为 的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;
的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;(3)根据(2)中的结论,猜测椭圆
 的“左特征点”的位置.
的“左特征点”的位置.(1) 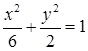 (2)
(2) 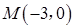 (3) 左准线与
(3) 左准线与 轴的交点
轴的交点
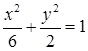 (2)
(2) 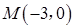 (3) 左准线与
(3) 左准线与 轴的交点
轴的交点本试题主要是运用椭圆的几何性质得到椭圆方程,然后结合新定义得到直线与 椭圆的方程联立,结合韦达定理表示,然后得到左特征点。同时利用椭圆的准线返程的得到交点,进而猜测左特征点。
(1)由条件知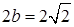 ,可设椭圆方程为
,可设椭圆方程为
又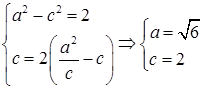
(2))设左特征点为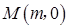 ,左焦点为
,左焦点为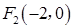 ,
,
可设直线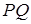 的方程为
的方程为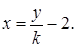
联立直线与椭圆方程的得到关系式,进而得到韦达定理,利用角平分线的性质得到结论。
(3)因为椭圆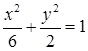 的左准线与
的左准线与 轴的交点为
轴的交点为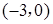 ,
,
故猜测椭圆 的左特征点为左准线与
的左特征点为左准线与 轴的交点。
轴的交点。
解:(1)由条件知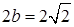 ,可设椭圆方程为
,可设椭圆方程为
又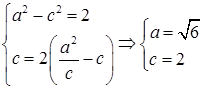
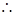 椭圆方程为
椭圆方程为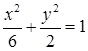 …………4分
…………4分
(2)设左特征点为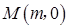 ,左焦点为
,左焦点为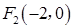 ,
,
可设直线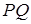 的方程为
的方程为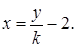
由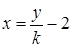 与
与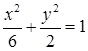 ,消去
,消去 得
得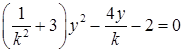
又设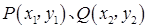 ,则
,则
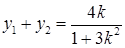 ①
①
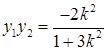 ② …………6分
② …………6分
因为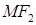 为
为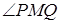 的角平分线,所以
的角平分线,所以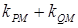
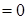 ,即
,即
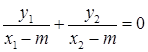 ③
③
将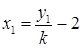 与
与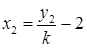 代入③化简,得
代入③化简,得
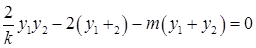 ④
④
再将①②代入④得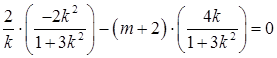
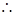
 即左特征点为
即左特征点为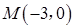 …………10分
…………10分
(3)因为椭圆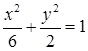 的左准线与
的左准线与 轴的交点为
轴的交点为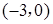 ,
,
故猜测椭圆 的左特征点为左准线与
的左特征点为左准线与 轴的交点. …………12分
轴的交点. …………12分
(1)由条件知
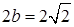 ,可设椭圆方程为
,可设椭圆方程为
又
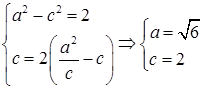
(2))设左特征点为
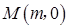 ,左焦点为
,左焦点为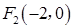 ,
,可设直线
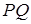 的方程为
的方程为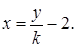
联立直线与椭圆方程的得到关系式,进而得到韦达定理,利用角平分线的性质得到结论。
(3)因为椭圆
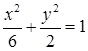 的左准线与
的左准线与 轴的交点为
轴的交点为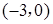 ,
,故猜测椭圆
 的左特征点为左准线与
的左特征点为左准线与 轴的交点。
轴的交点。解:(1)由条件知
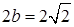 ,可设椭圆方程为
,可设椭圆方程为
又
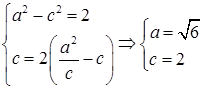
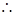 椭圆方程为
椭圆方程为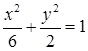 …………4分
…………4分(2)设左特征点为
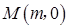 ,左焦点为
,左焦点为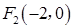 ,
,可设直线
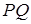 的方程为
的方程为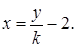
由
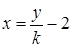 与
与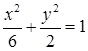 ,消去
,消去 得
得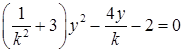
又设
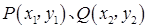 ,则
,则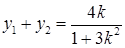 ①
① 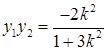 ② …………6分
② …………6分因为
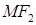 为
为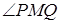 的角平分线,所以
的角平分线,所以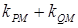
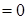 ,即
,即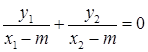 ③
③将
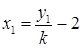 与
与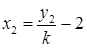 代入③化简,得
代入③化简,得 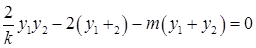 ④
④再将①②代入④得
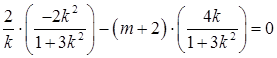
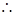
 即左特征点为
即左特征点为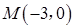 …………10分
…………10分(3)因为椭圆
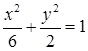 的左准线与
的左准线与 轴的交点为
轴的交点为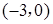 ,
,故猜测椭圆
 的左特征点为左准线与
的左特征点为左准线与 轴的交点. …………12分
轴的交点. …………12分
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 轴上,长轴长为4,短轴长为2,则椭圆方程是( )
轴上,长轴长为4,短轴长为2,则椭圆方程是( )

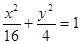

 与双曲线
与双曲线 的左右两支分别交于
的左右两支分别交于 、
、 两点,与双曲线
两点,与双曲线 的右准线相交于
的右准线相交于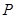 点,
点, 为右焦点,若
为右焦点,若 ,又
,又 ,则实数
,则实数 的值为
的值为
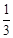

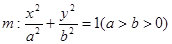 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为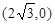 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且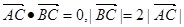
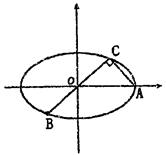
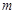 的方程;
的方程;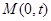 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,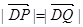 ,求实数t的取值范围.
,求实数t的取值范围. 的左、右顶点分别A、B,椭圆过点(0,1)且离心率
的左、右顶点分别A、B,椭圆过点(0,1)且离心率 .
. 轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线
轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线 轴,连结AQ并延长交直线
轴,连结AQ并延长交直线 于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
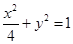 上,则
上,则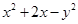 的最大值为
的最大值为 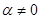 的直线
的直线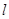 过椭圆
过椭圆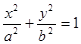
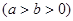 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则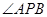 为 ( )
为 ( )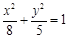 的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.  和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 点,若直线
点,若直线 恰与圆
恰与圆