题目内容
已知 ,
, .
.
(Ⅰ)设 ,求函数
,求函数 的图像在
的图像在 处的切线方程;
处的切线方程;
(Ⅱ)求证: 对任意的
对任意的 恒成立;
恒成立;
(Ⅲ)若 ,且
,且 ,求证:
,求证: .
.
解:(1) ,
, ,则
,则
 ,∴
,∴ 图像在
图像在 处的切线方程为
处的切线方程为 即
即
(2)令 ,
,
则
∵ 与
与 同号 ∴
同号 ∴ ∴
∴
∴ ∴
∴ 在
在 单调递增
单调递增
又 ,∴当
,∴当 时,
时, ;当
;当 时,
时,
∴ 在
在 单调递减,在
单调递减,在 单调递增 ∴
单调递增 ∴
∴ 即
即 对任意的
对任意的 恒成立
恒成立
(3)由(2)知
则

由柯西不等式得
∴

同理



三个不等式相加即得证。

练习册系列答案
相关题目
 中,角A,B,C所对的边长分别为a,b,c.若
中,角A,B,C所对的边长分别为a,b,c.若 .则角C等于( )
.则角C等于( ) B.
B. C.
C. D.
D.
 垂直的抛物线
垂直的抛物线 的切线方程为 .
的切线方程为 . 的两个焦点为
的两个焦点为 、
、 ,其中一条渐近线方程为
,其中一条渐近线方程为 ,
, 为双曲线上一点,且满足
为双曲线上一点,且满足 (其中
(其中 为坐标原点),若
为坐标原点),若 、
、 、
、 成等比数列,则双曲线
成等比数列,则双曲线 的方程为
的方程为 B.
B. C.
C. D.
D.
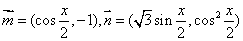 ,设函数
,设函数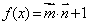
 的单调递增区间;
的单调递增区间;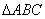 中,角
中,角 、
、 、
、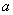 、
、 、
、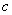 ,且满足
,且满足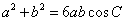 ,
,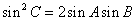 ,求
,求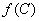 的值.
的值. 在区间
在区间 上存在一个零点,则
上存在一个零点,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D. 的函数
的函数 满足
满足 当
当 时,
时, ,若
,若 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B. 
 D.
D. 
 和
和 是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 ,则过A、B、C三点的圆面积为( )
,则过A、B、C三点的圆面积为( ) B.
B. C.
C.  D.
D. 
 所对的角分别为
所对的角分别为 ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.