题目内容
 .若对任意
.若对任意 ,总存在
,总存在 ,使得f(x1)≥g(x2),则m的取值范围是________.
,使得f(x1)≥g(x2),则m的取值范围是________.
(-∞, ]
]
分析:由对任意 ,总存在
,总存在 ,使得f(x1)≥g(x2),知f(x1)min≥g(x2)min,由此能求出m的取值范围.
,使得f(x1)≥g(x2),知f(x1)min≥g(x2)min,由此能求出m的取值范围.
解答:∵对任意 ,总存在
,总存在 ,使得f(x1)≥g(x2),
,使得f(x1)≥g(x2),
∴f(x1)min≥g(x2)min,
∵ ,
,
∴f′(x)=2x-2m, ,
,
由f′(x)=2x-2m=0,得x=m,
∵ ,f(m)=-m2+m,
,f(m)=-m2+m,
∴f(x1)min=f(2)=4-3m.
∵ <0,
<0,
∴ 时,g(x2)是减函数,
时,g(x2)是减函数,
∴g(x2)min=g(2)= =-
=- ,
,
∵f(x1)min≥g(x2)min,
∴4-3m≥- .
.
解得m≤ .
.
故答案为:(-∞, ].
].
点评:本题考查函数恒成立问题的应用,解题时要认真审题,注意等价转化思想和导数性质的灵活运用.
 ]
]分析:由对任意
 ,总存在
,总存在 ,使得f(x1)≥g(x2),知f(x1)min≥g(x2)min,由此能求出m的取值范围.
,使得f(x1)≥g(x2),知f(x1)min≥g(x2)min,由此能求出m的取值范围.解答:∵对任意
 ,总存在
,总存在 ,使得f(x1)≥g(x2),
,使得f(x1)≥g(x2),∴f(x1)min≥g(x2)min,
∵
 ,
,∴f′(x)=2x-2m,
 ,
,由f′(x)=2x-2m=0,得x=m,
∵
 ,f(m)=-m2+m,
,f(m)=-m2+m,∴f(x1)min=f(2)=4-3m.
∵
 <0,
<0,∴
 时,g(x2)是减函数,
时,g(x2)是减函数,∴g(x2)min=g(2)=
 =-
=- ,
,∵f(x1)min≥g(x2)min,
∴4-3m≥-
 .
.解得m≤
 .
.故答案为:(-∞,
 ].
].点评:本题考查函数恒成立问题的应用,解题时要认真审题,注意等价转化思想和导数性质的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
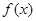 满足
满足 ,当
,当 时,
时,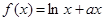
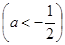 ,当
,当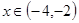 时,
时, 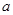 的值;
的值;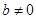 ,函数
,函数 ,
,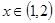 .若对任意的
.若对任意的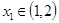 ,总存在
,总存在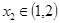 ,使
,使 ,求实数
,求实数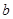 的取值范围.
的取值范围. ,
, ,
, 在
在 上的值域是 ;
上的值域是 ; ,总存在
,总存在 ,使得
,使得 ,则实数
,则实数 的取值范围
的取值范围 .
. 的单调区间;
的单调区间; ,若对任意
,若对任意 ,总存在
,总存在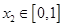 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.