题目内容
已知函数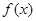 满足
满足 ,当
,当 时,
时,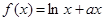
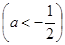 ,当
,当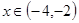 时,
时, 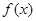 的最大值为-4.
的最大值为-4.
(I)求实数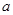 的值;
的值;
(II)设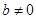 ,函数
,函数 ,
,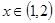 .若对任意的
.若对任意的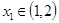 ,总存在
,总存在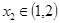 ,使
,使 ,求实数
,求实数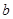 的取值范围.
的取值范围.
【答案】
(I)  ; (II)
; (II) 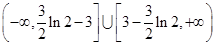
【解析】
试题分析:(I) 因为函数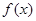 满足
满足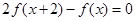 ,当
,当 ,所以可得f(x)=2f(x+2)=4f(x+4)当x
,所以可得f(x)=2f(x+2)=4f(x+4)当x (-4,-2),则x+4
(-4,-2),则x+4 (0,2)这样就可以f(x)=4f(x+4)=4ln(x+4)+4
(0,2)这样就可以f(x)=4f(x+4)=4ln(x+4)+4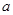 (x+4).所以通过求导可求出f(x)的导数,再根据
(x+4).所以通过求导可求出f(x)的导数,再根据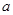 的取值范围求出函数的单调区间即可求出最大值.从而解出
的取值范围求出函数的单调区间即可求出最大值.从而解出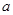 的值.
的值.
(II)假设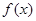 的值域为A,
的值域为A,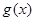 的值域为B,则由已知,对于任意的
的值域为B,则由已知,对于任意的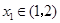
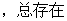
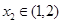 ,使
,使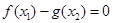 得,
得, 即函数f(x)值域的范围比函数g(x)值域的范围小即可.对于函数g(x)的单调性要考虑b的值.再根据,
即函数f(x)值域的范围比函数g(x)值域的范围小即可.对于函数g(x)的单调性要考虑b的值.再根据, 即可得结论.
即可得结论.
试题解析:(I)由已知,得2f(x+2)=f(x),所以f(x)=2f(x+2)=4f(x+4).又因为x (0,2)时,f(x)=lnx+
(0,2)时,f(x)=lnx+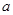 x.设x
x.设x (-4,-2),则x+4
(-4,-2),则x+4 (0,2).所以f(x+4)=ln(x+4)+
(0,2).所以f(x+4)=ln(x+4)+ 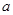 (x+4).所以x
(x+4).所以x (-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4
(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4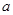 (x+4).所以
(x+4).所以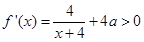 .因为x
.因为x (-4,-2).所以
(-4,-2).所以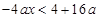 .因为
.因为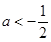 .所以
.所以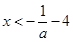 .又由
.又由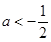 可得
可得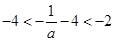 .所以f(x)在
.所以f(x)在 上是增函数,在
上是增函数,在 上是减函数.所以
上是减函数.所以 .所以
.所以 .
.
(II)设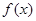 的值域为A,
的值域为A,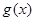 的值域为B,则由已知,对于任意的
的值域为B,则由已知,对于任意的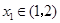
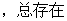
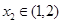 ,使
,使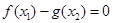 得,
得, .
.
由(I)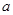 =-1,当
=-1,当 时,
时,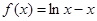 ,
,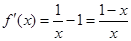 ,
,
∵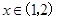 ,∴
,∴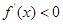 ,
,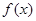 在
在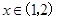 上单调递减函数,
上单调递减函数,
∴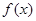 的值域为 A=
的值域为 A=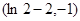
∵ ,
,
∴(1)当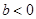 时,
时,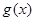 在
在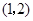 上是减函数,此时,
上是减函数,此时,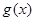 的值域为
的值域为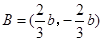 ,
,
为满足 ,又
,又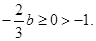 ∴
∴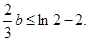 即
即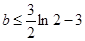 . 12分
. 12分
(2)当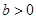 时,
时,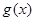 在
在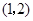 上是单调递增函数,此时,
上是单调递增函数,此时,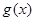 的值域为
的值域为 ,为满足
,为满足 ,又,∴
,又,∴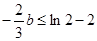 ,∴
,∴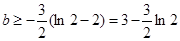 ,
,
综上可知b的取值范围是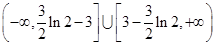 .
.
考点:1.函数的周期性问题.2.函数的最值.3.两个函数的值域的问题.4.含参数函数的最值问题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
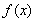
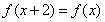

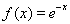
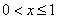

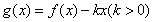


 满足
满足 ,且
,且 时,
时, ,若在区间[-1,3]内,函数
,若在区间[-1,3]内,函数 有4个零点,则实数
有4个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 满足
满足 当
当 时总有
时总有 ,
, ,则实数
,则实数 的取值范围是___ ____.
的取值范围是___ ____. 满足:①定义域为
满足:①定义域为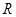 ;②对任意
;②对任意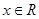 ,有
,有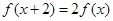 ;③当
;③当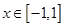 时,
时,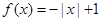 .则方程
.则方程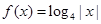 在区间
在区间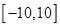 内的解的个数
内的解的个数