题目内容
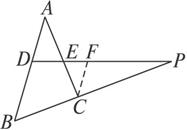
如图求证:BP∶CP=BD∶CE.
图
证明:过C作CF∥AB,交DP于F,则BP∶CP=BD∶CF,
∠EFC=∠ADE.
∵AD=AE,
∴∠ADE=∠AED.
∴∠AED=∠CFE.
∵∠AED=∠CEF,
∴∠CEF=∠CFE.
∴CE=CF.
∴BP∶CP=BD∶CE.

练习册系列答案
相关题目
题目内容
如图求证:BP∶CP=BD∶CE.

图
证明:过C作CF∥AB,交DP于F,则BP∶CP=BD∶CF,
∠EFC=∠ADE.
∵AD=AE,
∴∠ADE=∠AED.
∴∠AED=∠CFE.
∵∠AED=∠CEF,
∴∠CEF=∠CFE.
∴CE=CF.
∴BP∶CP=BD∶CE.
