题目内容
已知点
在椭圆
上, 以为圆心的圆与
轴相切于
椭圆的右焦点
.
(1)若圆与
轴相切,求椭圆的离心率；
(2)若圆与轴相交于
两点,且
是边长为2的正三角形，求椭圆的方程.
解：(1)设
，圆M的半径为. 依题意得
将
代入椭圆方程得：
，所以
，又
从而得 
，两边除以
得：
解得：
，因为 
，
所以 
. 6分(也可用定义求a)
(2)因为是边长为2的正三角形，所以圆M的半径
，
M到圆轴的距离
又由(1)知：
，
所以，
，
又因为 
,解得：
, 
所求椭圆方程是：
12分
练习册系列答案
名校课堂系列答案
相关题目
为椭圆
上一定点，过点A作两条直线与椭圆交于B、C两点.若直线AB、AC与x轴围成以点A为顶点的等腰三角形，求直线BC的斜率，并求在什么条件下△ABC的面积最大？最大面积是多少？
的右焦点为
，
点在椭圆上，以
轴相切，且同时与
轴相切于椭圆的右焦点
的离心率为 ．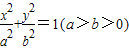
的右焦点为F，P点在椭圆上，以P点为圆心的圆与y轴相切，且同时与x轴相切于椭圆的右焦点F，则椭圆
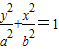的离心率为 ．