题目内容
已知点
解析: (1)将点 坐标代入椭圆方程得n=6 ∴椭圆方程为
坐标代入椭圆方程得n=6 ∴椭圆方程为 ①
①
由题设知等腰三角形ABC的两腰不能与x轴垂直,故设两腰AB、AC所在直线的斜率分别为 ,
, ,
,
则直线AB的方程为 ② 直线AC的方程为
② 直线AC的方程为 ③
③
∴由①②联立解得点B坐标为 ∴由①③联立解得点C坐标为
∴由①③联立解得点C坐标为
由题设知
∴直线BC的斜率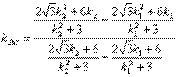



(2)设直线BC的方程为 ④
④ 
④代入椭圆方程 得
得
∴判别式△>0 ⑤ 且
⑤ 且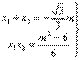
∴

 ⑥
⑥
又点A到直线BC的距离
∴△ABC的面积

当且仅当 时等号成立 ∴
时等号成立 ∴ ,当且仅当
,当且仅当 (满足⑤式)时取得.
(满足⑤式)时取得.
于是可知,当 或
或 时,△ABC的面积S取得最大值
时,△ABC的面积S取得最大值 ,
,
此时,直线BC的方程为 ,即
,即 .
.
此时又易知BC∥OA(O为原点),B、C两点恰好分别为长轴、短轴的端点.
由题设知等腰三角形ABC的两腰不能与x轴垂直,故设两腰AB、AC所在直线的斜率分别为
则直线AB的方程为
∴由①②联立解得点B坐标为
由题设知
∴直线BC的斜率
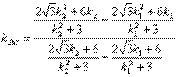
(2)设直线BC的方程为
④代入椭圆方程
∴判别式△>0
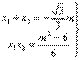
∴
又点A到直线BC的距离
∴△ABC的面积
当且仅当
于是可知,当
此时,直线BC的方程为
此时又易知BC∥OA(O为原点),B、C两点恰好分别为长轴、短轴的端点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分12分)
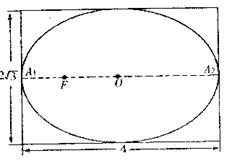
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.
 为圆
为圆 上的动点,且
上的动点,且 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 、
、 两点。
两点。 ,使得
,使得 总能被
总能被 为曲线
为曲线 在圆
在圆 上,
上, ,曲线
,曲线
 ,直线
,直线 , ………………3分
, ………………3分  ,可得
,可得 
 ,∴
,∴
 ,
,  ,则
,则 ,
,  得到。
得到。 ,
, ,
, , ………………10分
, ………………10分 ,
, ,
,  ,即只要
,即只要 ………………12分
………………12分  时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 ,使得
,使得 总能被
总能被 轴平分
轴平分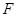 是椭圆
是椭圆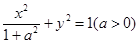 的右焦点,点
的右焦点,点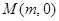 、
、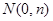 分别是
分别是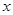 轴、
轴、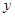 轴上的动点,且满足
轴上的动点,且满足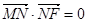 .若点
.若点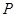 满足
满足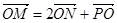 .
.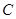 的方程;
的方程;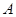 、
、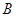 两点,直线
两点,直线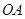 、
、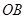 与直线
与直线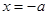 分别交于点
分别交于点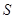 、
、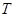 (
(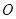 为坐标原点),试判断
为坐标原点),试判断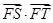 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.