题目内容
巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:
| | 男生 | 女生 | 合计 |
| 收看 | 10 | | |
| 不收看 | | 8 | |
| 合计 | | | 30 |
已知在这30名同学中随机抽取1人,抽到“通过电视收看世界杯”的学生的概率是
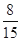 .
.(I)请将上面的列联表补充完整,并据此资料分析“通过电视收看世界杯”与性别是否有关?
(II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.
 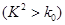 | 0.100 | 0.050 | 0.010 |
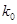 | 2.706 | 3.841 | 6.635 |
(参考公式:
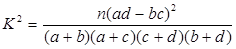 ,
, 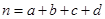 )
)
(Ⅰ)没有充足的理由认为“通过电视收看世界杯”与性别有关 ;(Ⅱ) .
.
解析试题分析:
解题思路:(Ⅰ)补充表格,套用 公式求值,利用临界值表进行判定;(Ⅱ)利用超几何分布的概率公式求概率,再进一步求数学期望.
公式求值,利用临界值表进行判定;(Ⅱ)利用超几何分布的概率公式求概率,再进一步求数学期望.
规律总结:1.利用独立性检验思想判断两个变量间的相关关系,要牢记公式与临界值表;2.利用概率或随机变量的分布列以及期望、方差解决应用题时,要注意随机变量的实际意义.
试题解析:(Ⅰ) 男生 女生 合计 收看 10 6 16 不收看 6 8 14 合计 16 14 30
由已知数据得:
所以,没有充足的理由认为“通过电视收看世界杯”与性别有关 .
(Ⅱ) 的可能取值为
的可能取值为
 ,
,
所以 的分布列为:
的分布列为:
0 1 2 



 的均值为:
的均值为:
 阅读快车系列答案
阅读快车系列答案某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数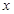 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间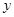 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
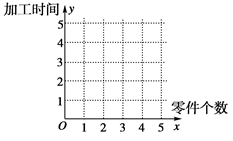
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出
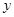 关于
关于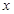 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;(3)试预测加工
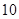 个零件需要多少时间?
个零件需要多少时间?参考公式:回归直线
 ,其中
,其中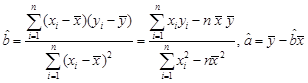 .
.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
序号 | 分组睡眠时间 | 组中值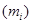 | 频数 (人数) | 频率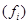 |
| 1 | 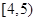 | 4.5 | 80 | ( ) |
| 2 | 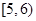 | 5.5 | 520 | 0.26 |
| 3 | 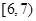 | 6.5 | 600 | 0.30 |
| 4 | 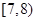 | 7.5 | ( ) | ( ) |
| 5 | 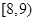 | 8.5 | 200 | 0.10 |
| 6 | 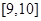 | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整;
(2)画出频率分布直方图;
(3)为了对数据举行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图,求输出的
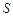 值。
值。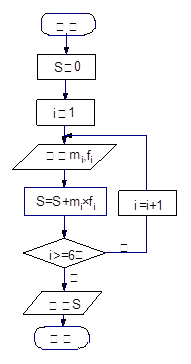
某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查,
统计数据如下表所示:
| | 积极参加班级工作 | 不太积极参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
试运用独立性检验的思想方法分析:学生的学习积极性与对待班级的态度是否有关系?
|
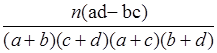
| P(K2≥k0 ) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
近年来,我国很多城市都出现了严重的雾霾天气.为了更好地保护环境,2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) |
| 第一组 | (0,35] | 24 |
| 第二组 | (35,75] | 48 |
| 第三组 | (75,115] | 12 |
| 第四组 | >115 | 6 |
(1)在这
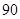 天中抽取
天中抽取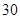 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?(2)在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.
 表示该班两个学生的百米测试成绩,已知
表示该班两个学生的百米测试成绩,已知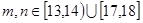 ,求事件
,求事件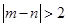 的概率.
的概率.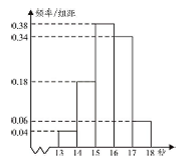



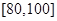 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在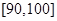 之间的概率;
之间的概率;