题目内容
7．命题p：关于x的不等式x2+（a-1）x+a2≤0的解集为∅，命题q：函数y=（2a2-a）x为增函数，若p，q至少有一个是真命题，求实数a的取值范围．分析 分别求出命题p和命题q为真命题时，a的取值范围，再求出p，q全为假命题时，a的取值范围，进而可得p，q至少有一个是真命题，实数a的取值范围．
解答 解：若命题p为真命题，
即关于x的不等式x2+（a-1）x+a2≤0的解集为∅，
则△=（a-1）2-4a2＜0，
解得：a∈（-∞，-1）∪（$\frac{1}{3}$，+∞），
若命题q为真命题，
即函数y=（2a2-a）x为增函数，
则2a2-a＞1，
解得：a∈（-∞，-$\frac{1}{2}$）∪（1，+∞），
若p，q全为假命题，
则a∈[-$\frac{1}{2}$，$\frac{1}{3}$]，
故p，q至少有一个是真命题时，
a∈（-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，+∞）
点评 本题考查的知识点是命题的真假判断与应用，复合命题，二次不等式的解法，指数函数的图象和性质，难度中档．
练习册系列答案
相关题目
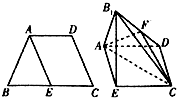已知四边形ABCD满足AD∥BC，BA=AD=DC=$\frac{1}{2}$BC=a，E是BC的中点，将△BAE沿AE翻折成△B1AE，使面B1AE⊥面AECD，F为B1D的中点．
18．在区间（-∞，1）上是增函数的是（ ）
| A． | y=$\frac{1}{x-1}$ | B． | y=-x2+2x-1 | C． | y=log2（1-x） | D． | y=2${\;}^{\frac{1}{x}}$ |