题目内容
已知函数
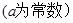
(1）是否存在实数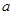
,使函数
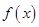是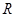
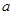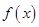上的奇函数,若不存在,说明理由,若存在实数,求函数的值域；
(2)探索函数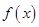的单调性，并利用定义加以证明。
【答案】
【解析】略
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
小学学习好帮手系列答案小学同步三练核心密卷系列答案题目内容
已知函数
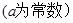
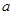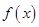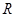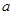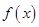(1）是否存在实数,使函数是上的奇函数,若不存在,说明理由,若存在实数,求函数的值域；
(2)探索函数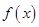的单调性，并利用定义加以证明。
【解析】略
小学学习好帮手系列答案小学同步三练核心密卷系列答案
的定义域;
轴;
满足什么条件时,
在
上恒取正值.
时，求函数
的最值；
使
的图象与
无公共点.
的图像在[a,b]上连续不断，定义：
，
，其中
表示函数
在D上的最小值，
表示函数
对任意的
成立，则称函数
上的“k阶收缩函数”
，试写出
，
的表达式；
试判断
，函数
是[0,b]上的2阶收缩函数，求b的取值范围
(
)
的单调性;
使得函数
上有最小值恰为
? 若存在,求出