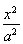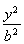题目内容

已知椭圆： $数学公式$ （a＞b＞0）的左、右焦点分别为F₁、F₂，以F₁为顶点，F₂为焦点的抛物线经过椭圆短轴的两端点，则a：b=________．

$\text{[math]}$
分析：写出椭圆的两个焦点及椭圆的短轴的端点坐标，根据已知条件求出抛物线的准线方程，利用抛物线的定义椭圆的短轴的端点到抛物线的焦点距离与到其准线的距离相等，列出方程得到a：b的值．
解答：根据已知得F₁（-c，0），F₂（c，0），椭圆的短轴的端点坐标为（0，b）
因为抛物线以F₁为顶点，F₂为焦点，
所以抛物线的准线方程为x=-3c
又抛物线的定义得到 $\text{[math]}$
即b²=8c²
即8a²=9b²
所以a：b= $\text{[math]}$
故答案为 $\text{[math]}$
点评：本题考查抛物线的定义及椭圆中三个参数a，b，c的关系：a²=b²+c²，是一道中档题．

练习册系列答案

教材解读与拓展系列答案

教材快线系列答案

教材完全学案系列答案

精析巧练系列答案

今日课堂课时作业系列答案

金版卷王课程探究大试卷系列答案

金榜之路系列答案

金点中考系列答案

金海全A突破系列答案

金考卷45套汇编系列答案

相关题目

+y2=1
（1）过椭圆上点P作x轴的垂线PD，D为垂足，当点P在椭圆上运动时，求线段PD中点M的轨迹方程；
（2）若直线x-y+m=0与已知椭圆交于A、B两点，R（0，1），且|RA|=|RB|，求实数m的值．

=1(0＜b＜2)的离心率为

．
（1）求此椭圆的方程；
（2）若直线x-y+m=0与已知椭圆交于A，B两点，P（0，1），且|PA|=|PB|，求实数m的值．

已知椭圆ε：

（a>b>0），动圆

，其中ba. 若A是椭圆ε上的点，B是动圆

上的点，且使直线AB与椭圆ε和动圆

均相切，求A、B两点的距离

已知椭圆=1（a＞b＞0）的离心率为，,则椭圆方程为（　　）

A.=1

B.=1

C.=1

D.=1

已知椭圆C:+=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.

(1)求椭圆C的标准方程及离心率;

(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.