题目内容
已知椭圆C: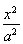 +
+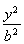 =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.
【答案】
(1)  +
+ =1 e=
=1 e= (2)
(2)  (
( ,
, )
)
【解析】
解:(1)由题设得
解得a=2,b= ,c=1.
,c=1.
故C的方程为 +
+ =1,离心率e=
=1,离心率e= .
.
(2)直线F1A的方程为y= (x+1),
(x+1),
设点O关于直线F1A对称的点为M(x0,y0),
则 ⇒
⇒
所以点M的坐标为(- ,
, ).
).
∵|PO|=|PM|,|PF2|+|PO|=|PF2|+|PM|≥|MF2|,
|PF2|+|PO|的最小值为
|MF2|= =
= .
.
直线MF2的方程为y= (x-1),
(x-1),
即y=- (x-1).
(x-1).
由 ⇒
⇒
所以此时点P的坐标为( ,
, ).
).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
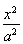



 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).