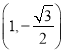题目内容
【题目】函数![]() .
.
(1)当![]() ,
, ![]() 时,求
时,求![]() 的单调减区间;
的单调减区间;
(2)![]() 时,函数
时,函数![]() ,若存在
,若存在![]() ,使得
,使得![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析 (2)![]()
【解析】试题分析:
(1)原函数的导函数为![]() ,对实数n分类讨论可得:
,对实数n分类讨论可得:
①当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;
;
②当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;
;
③当![]() 时,减区间为
时,减区间为![]() .
.
(2)由题意结合恒成立的条件构造新函数设![]() ,结合函数h(t)的性质分类讨论可得实数
,结合函数h(t)的性质分类讨论可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
①当![]() 时,
时, ![]() ,此时
,此时![]() 的单调减区间为
的单调减区间为![]() ;
;
②当![]() 时,
时, ![]() 时,
时, ![]() ,此时
,此时![]() 的单调减区间为
的单调减区间为![]() ;
;
③当![]() 时,
时, ![]() 时,
时, ![]() ,此时减区间为
,此时减区间为![]() .
.
(2)![]() 时,
时, ![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
设![]() ,∴
,∴![]() ,∴
,∴![]() .
.
设![]() ,
,  ,
, ![]() ,
,
①当![]() 时,
时, ![]() ,
,
故![]() ,∴
,∴![]() 在
在![]() 上单调递增,因此
上单调递增,因此![]() ;
;
②当![]() 时,令
时,令![]() ,得:
,得: ![]() ,
, ![]() ,
,
由![]() 和
和![]() ,得:
,得: ![]() ,故
,故![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() .
.
综上所述, ![]() .
.

【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]()
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名学生组成一个样本,再从样本中抽出2名学生,记甲班被抽到的人数为ξ,求ξ的分布列和数学期望.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(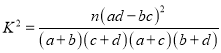 ,其中
,其中![]() )
)