题目内容
若函数f(x)=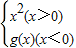 是奇函数,则函数g(x)的解析式是 .
是奇函数,则函数g(x)的解析式是 .
【答案】分析:利用函数奇偶性的定义进行转化求解即可.
解答:解:当x<0时,-x>0,所以此时f(-x)=(-x)2=x2,
因为函数f(x)是奇函数,所以f(-x)=(-x)2=x2=-f(x)=-g(x),
所以g(x)=-x2.
故答案为:-x2.
点评:本题主要考查函数奇偶性的应用,利用奇偶性讲变量进行转化是解决本题的关键.
解答:解:当x<0时,-x>0,所以此时f(-x)=(-x)2=x2,
因为函数f(x)是奇函数,所以f(-x)=(-x)2=x2=-f(x)=-g(x),
所以g(x)=-x2.
故答案为:-x2.
点评:本题主要考查函数奇偶性的应用,利用奇偶性讲变量进行转化是解决本题的关键.

练习册系列答案
相关题目
 是奇函数,则m为 .
是奇函数,则m为 .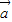 ,
,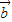 满足
满足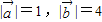 ,且
,且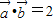 ,则
,则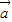 与
与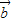 的夹角为
的夹角为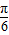 ;
;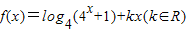 是偶函数,函数
是偶函数,函数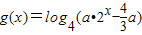 ,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞).
,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞). +a是奇函数,则实数a的值为( )
+a是奇函数,则实数a的值为( )
