题目内容
直线y=kx-2与抛物线y2=8x交于A、B两点,且AB中点的横坐标为2,则k的值为（ ）A.-1 B.2 C.2或-1 D.4
思路分析：∵直线y=kx-2与抛物线y2=8x交于两点，∴k≠0.
由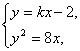
得k2x2-4kx-8x+4=0.∴x1+x2=
.
而A、B中点横坐标为2，∴
=4，解得k=-1或k=2.
而当k=-1时，方程k2x2-4kx-8x+4=0只有一个解，即A、B两点重合.
∴k≠-1.
答案：B
练习册系列答案
相关题目
题目内容
直线y=kx-2与抛物线y2=8x交于A、B两点,且AB中点的横坐标为2,则k的值为（ ）A.-1 B.2 C.2或-1 D.4
思路分析：∵直线y=kx-2与抛物线y2=8x交于两点，∴k≠0.
由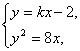得k2x2-4kx-8x+4=0.∴x1+x2=.
而A、B中点横坐标为2，∴=4，解得k=-1或k=2.
而当k=-1时，方程k2x2-4kx-8x+4=0只有一个解，即A、B两点重合.
∴k≠-1.
答案：B