题目内容
已知数列 的前n项和
的前n项和 ,则 ( )
,则 ( )
 的前n项和
的前n项和 ,则 ( )
,则 ( )A. = = | B. = = | C. = = | D. = = |
C
本题考查数列前n项和与通项关系,求通项的方法.
由 求
求 的方法:第一步:求
的方法:第一步:求 ;第二步:求
;第二步:求 时的
时的 ,第三步:验证
,第三步:验证 对
对 是否成立,若不成立,
是否成立,若不成立, 分段.
分段.
当 时,
时, 当
当 时,
时,

若
 综上:
综上:
 .故选C
.故选C
由
 求
求 的方法:第一步:求
的方法:第一步:求 ;第二步:求
;第二步:求 时的
时的 ,第三步:验证
,第三步:验证 对
对 是否成立,若不成立,
是否成立,若不成立, 分段.
分段.当
 时,
时, 当
当 时,
时,

若

 综上:
综上:
 .故选C
.故选C
练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 、
、 满足a1=1,a2=2,bn+1=3bn
满足a1=1,a2=2,bn+1=3bn ,bn=an+1-an.
,bn=an+1-an. 满足
满足 ,求数列
,求数列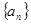 的公差为
的公差为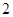 ,若
,若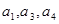 成等比数列, 则
成等比数列, 则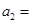 ( )
( )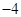



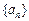 满足条件
满足条件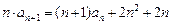 ,
,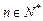 ,
,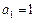 ,设
,设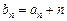

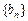 的通项公式;
的通项公式;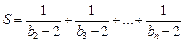 。(14分)
。(14分)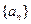 的前
的前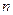 项和为
项和为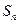 ,对一切
,对一切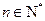 ,点
,点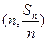 都在函数
都在函数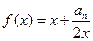 的图象上.
的图象上.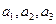 及数列
及数列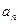 ;
;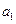 ),(
),(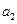 ,
,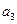 ),(
),(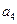 ,
,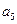 ,
,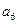 ),(
),(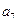 ,
,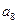 ,
,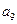 ,
,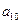 );(
);(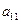 ),(
),(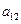 ,
,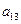 ),(
),(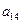 ,
,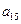 ,
,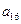 ),(
),(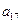 ,
,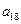 ,
,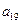 ,
,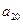 );(
);(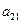 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为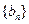 ,求
,求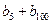 的值;
的值;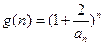 (
(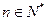 ),求证:
),求证: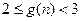 .
.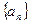 的各项都为正数,其前
的各项都为正数,其前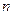 项和为
项和为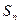 ,已知对任意
,已知对任意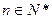 ,
,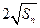 是
是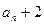 和
和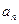 的等比中项.
的等比中项.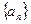 的通项公式;
的通项公式;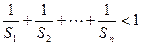 ;
;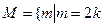 ,
,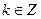 ,且
,且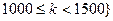 ,若存在
,若存在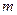 ∈
∈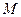 ,使对满足
,使对满足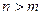 的一切正整数
的一切正整数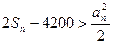 恒成立,求这样的正整数
恒成立,求这样的正整数 中,若
中,若 ,则
,则 的值为 ( )
的值为 ( )  为等差数列,且
为等差数列,且 ,
, 。
。 的
的 最大值是 。
最大值是 。