题目内容
如图,在长方形ABCD中,AB=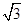 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 

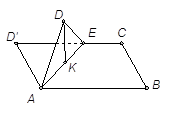
A. | B. | C. | D. |
A
解析试题分析:根据△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,可知D′K⊥AE,所以K的轨迹是以AD′为直径的一段圆弧D′K,求出圆心角∠D′OK,即可求得K所形成轨迹的长度. 
解:由题意,D′K⊥AE,所以K的轨迹是以AD′为直径的一段圆弧D′K,设AD′的中点为O,,∵长方形ABCD′中,AB=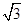 ,BC=1,∴∠D′AC=60°∴∠D′OK=120°=
,BC=1,∴∠D′AC=60°∴∠D′OK=120°= π,∴K所形成轨迹的长度为
π,∴K所形成轨迹的长度为 π×
π× =
= 故选A.
故选A.
考点:几何中的轨迹
点评:本题以平面图形的翻折为载体,考查立体几何中的轨迹问题,考查弧长公式的运用,解题的关键是利用D′K⊥AE,从而可知K的轨迹是以AD′为直径的一段圆弧D′K

练习册系列答案
相关题目
已知: ,
, ,
, ,则
,则 与
与 的位置关系是( )
的位置关系是( )
A. | B. |
C. , , 相交但不垂直 相交但不垂直 | D. , , 异面 异面 |
已知 、
、 是不同的平面,
是不同的平面, 、
、 是不同的直线,则下列命题不正确的( )
是不同的直线,则下列命题不正确的( )
A.若 ∥ ∥ 则 则 | B.若 ∥ ∥ 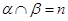 ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , , ,则 ,则 | D.若  则 则 ∥ ∥ |
已知 是两两不重合的三个平面,下列命题中错误的是( )
是两两不重合的三个平面,下列命题中错误的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
设 为两条直线,
为两条直线,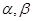 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若 , , 则 则 | D.若 则 则 |
对于两条不相交的空间直线 和
和 ,必定存在平面
,必定存在平面 ,使得 ( )
,使得 ( )
A. | B. | C. | D. |
设 为两条直线,
为两条直线, 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若 与 与 所成的角相等,则 所成的角相等,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
 ,则这个二面角的大小为( )
,则这个二面角的大小为( )




 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=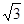 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 

