题目内容

若△ABC面积S=（a2+b2-c2）则∠C=（ ）
A．
B．
C．
D．
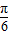
【答案】分析：先由余弦定理求得a2+b2-c2=2abcosC，代入题设三角形面积的表达式，进而利用三角形面积公式建立等式求得cosC和sinC的关系求得C．
解答：解：由余弦定理可知cosC=
∴a2+b2-c2=2abcosC
∵S=absinC=（a2+b2-c2）=abcosC
∴sinC=cosC
∵0＜C＜π
∴C=
故选C
点评：本题主要考查了余弦定理的应用．解题的过程中主要是利用了余弦定理的变形公式，把边的问题转化为角的问题．
练习册系列答案
相关题目
已知a、b、c分别是△ABC的三个内角A、B、C的对边．
（1）若△ABC面积S△ABC=
3
2
，c=2，A=60°，求a、b的值；
（2）若a=ccosB，且b=csinA，试判断△ABC的形状．
若△ABC面积S=
1
4
（a2+b2-c2）则∠C=（　　）
A、
π
2
B、
π
3
C、
π
4
D、
π
6
已知a、b、c分别是△ABC的三个内角A、B、C所对的边．若△ABC面积S△ABC=
3
2
，c=2，A=60°，则b的值为
1
1
；a的值为
3
3
．
已知a、b、c分别是△ABC的三个内角A、B、C所对的边；
（1）若△ABC面积S△ABC=
3
2
，c=2，且A、B、C成等差数列，求a、b的值；
（2）若acosA=bcosB，试判断△ABC的形状．
已知a、b、c分别是△ABC的三个内角A、B、C所对的边，若△ABC面积S△ABC=
3
2
，c=2，A=60°，求a、b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网